Modelos de agrupamento são técnicas de aprendizado não supervisionado usadas para organizar dados em grupos (clusters) de forma que elementos semelhantes fiquem no mesmo grupo e diferentes fiquem em grupos distintos. Eles são amplamente aplicados quando não há rótulos ou classes pré-definidas nos dados. O K-means é um dos algoritmos de agrupamento mais conhecidos. Ele funciona dividindo os dados em K grupos, de acordo com a proximidade entre os pontos e os centróides (as médias de cada grupo). O processo é repetido até que os centróides se estabilizam, ou seja, até a convergência.

Esse modelo é aplicável nas seguintes situações:
- Segmentação de clientes em marketing;
- Agrupamento de documentos ou notícias semelhantes;
- Análise de padrões em dados de saúde, sensores ou redes sociais;
- Detecção de anomalias ou comportamentos fora do padrão.
Para iniciar tarefas de agrupamento de dados é necessário importar algumas bibliotecas, para garantir o funcionamento pleno (plotagem de gráficos, uso de funções matemáticas). Sendo elas:
pandas → manipulação de dados;
numpy → operações matemáticas;
matplotlib → visualização gráfica;
KMeans → algoritmo de agrupamento;
StandardScaler → normalização;
train_test_split → separação de conjuntos de treino e teste

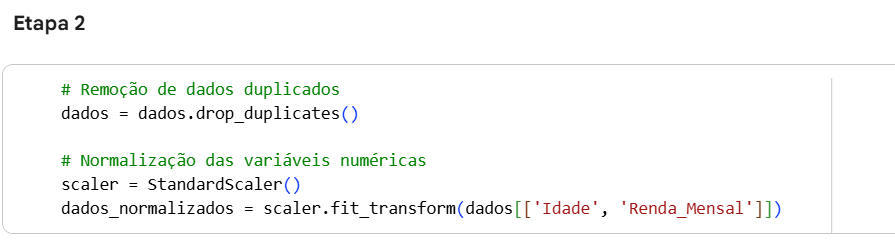
Com a etapa de limpeza e pré-processamento garantimos a qualidade dos dados antes da mineração. Consiste em identificar e tratar valores ausentes, usando técnicas como imputação pela média, moda ou por similaridade, além de corrigir inconsistências causadas por erros de digitação ou padronização entre sistemas.

Também envolve a integração de dados de diferentes fontes e a transformação para uniformizar formatos, capitalização e unidades. Esse processo torna o conjunto de dados coerente, confiável e pronto para o agrupamento. Algumas operações que podem ser aplicadas a essa etapa são:
- Dicionário para substituição de dados faltantes
- Verificação de valores nulos
- Verificação de outliers (remoção ou não)
- Normalização de valores numéricos
- Conversão de dados (exemplo: One hot enconding)
É importante selecionar as variáveis para garantir que o modelo use apenas os atributos mais relevantes, evitando ruído e melhorando o desempenho. Reduzindo a complexidade, aumentando a precisão e facilitando a interpretação dos resultados. Pode ser feita com base em análise estatística, métodos automáticos (como feature selection do scikit-learn) ou conhecimento do domínio, escolhendo as variáveis que realmente influenciam o problema.
Para executar o agrupamento, utilizamos apenas as variáveis numéricas relevantes para o problema e ajustamos o modelo K-means com K grupos.
O valor de K deve ser escolhido com base em métodos como o cotovelo (Elbow) ou o coeficiente de silhueta, e não apenas por ser menor que o número de amostras — embora, naturalmente, K não possa exceder o número total de observações (K ≤ n).
Dentro do conjunto de treino são realizadas as seguintes etapas para formar os grupos e ajustar o algoritmo:
- k é escolhido pelo usuário;
- Cada ponto da massa de dados é atribuído ao centróide mais próximo;
- A atribuição é feita de Seção3_GifResultados_Imagem1acordo com uma medida de distância;
- Cada coleção de pontos atribuídos a um centróide é um grupo;
- O centróide (cálculo da nova média) é atualizado refazendo-se as medidas de distância no próprio grupo;
- Os passos são repetidos até que o centróide de cada grupo permaneça estável, ou seja, nenhum objeto é trocado de grupo.

A partir dos resultados obtidos, conseguimos agrupar da melhor maneira, conforme as iterações ocorrem no algoritmo.

Após o ajuste do modelo, os centróides obtidos podem ser utilizados para atribuir novas observações ao cluster mais próximo, aplicando a mesma medida de distância usada no processo de agrupamento.
Essa etapa não tem o objetivo de avaliar generalização, como ocorre em modelos supervisionados, mas sim de verificar a estabilidade do padrão de agrupamento quando aplicado a dados inéditos — isto é, observar se a estrutura formada se mantém coerente para novos pontos.
Para avaliar a qualidade dos agrupamentos produzidos, utilizam-se métricas específicas que analisam simultaneamente a coerência interna dos clusters (o quão próximos os pontos de um mesmo grupo estão entre si) e a separação entre clusters (o quão distintos os grupos são no espaço).
Entre as métricas mais utilizadas estão:
mede o quão bem cada ponto está alocado ao seu grupo — valores próximos de 1 indicam boa separação.

Como é calculado?
Na fórmula nós temos os termos b(i) que representa o valor de separação, ou seja, é a distância média entre um ponto de dados ‘i’ e os pontos em qualquer outro cluster. Já a(i) representa a coesão, a distância média entre o ponto de dado e todos os outros pontos no mesmo cluster.
Avalia a compacidade e separação dos clusters — quanto menor o valor, melhor o agrupamento.

Como é calculado?
Para calcular o Índice de Davies-Bouldin (DBI) é necessário conhecer a similaridade máxima de todos os cluster i em relação aos cluster existentes, assim é possível fazer a média das similaridades. A medida de similaridade entre dois clusters é a razão da soma de suas dispersões individuais pela distância entre seus centróides. Portanto, é necessário calcular também a dispersão Intra-Cluster, que é a média da distância de cada ponto de dado de um cluster em relação ao centróide, e a separação Inter-Cluster, que é a distância entre centróides.


mede a razão entre dispersão entre e dentro dos grupos — valores maiores indicam melhor definição dos clusters.

Como é calculado?
A partir da definição de um centróide global, ou seja, a média das amostras no conjunto de dados, é possível calcular o SSb que é a distância quadrada entre o centróide do cluster e a média global, ponderada pelo número de pontos no cluster. Já o SSw é a distância quadrada entre os pontos e o centróide do seu próprio cluster.
Essas métricas auxiliam na comparação entre diferentes valores de K e na escolha do modelo mais adequado ao problema.


SILVA, Luiz Paulo Moreira. Dimensões do espaço. Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/dimensoes-espaco.htm. Acesso em: 14 fev. 2018.
REZENDE, Solange O.; MARCACINI, Ricardo M.; MOURA, Maria F. O uso da mineração de textos para extração e organização não supervisionada de conhecimento. Revista de Sistemas de Informação da FSMA, n. 7, p. 7–21, 2011.
NOGARÉ, Diego. Entenda o algoritmo K-means. Disponível em: https://diegonogare.net/2015/08/entendendo-como-funciona-o-algoritmo-de-cluster-k-means/. Acesso em: 5 nov. 2025.
DE CASTRO, Leandro Nunes; FERRARI, Daniel Godoy. Introdução à Mineração de Dados: Conceitos Básicos, Algoritmos e Aplicações. São Paulo: Saraiva, 2016.
HAN, Jiawei; KAMBER, Micheline. Data Mining: Concepts and Techniques. 2. ed. San Francisco: Elsevier, 2006.
SCIKIT-LEARN Developers. Clustering performance evaluation. Disponível em: https://scikit-learn.org/stable/modules/clustering.html#clustering-performance-evaluation. Acesso em: nov. 2025.
HASTIE, Trevor; TIBSHIRANI, Robert; FRIEDMAN, Jerome. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2. ed. New York: Springer, 2009.
GOOGLE COLAB. Notebook. Disponível em: https://colab.research.google.com/drive/1ZmPIAhsoeGtA_WEi8qqzUXsnJpZ26Zsc#scrollTo=UUxGMy3XbSiA. Acesso em: nov. 2025.