Classificação

O que é uma Árvore de Decisão? Qual a sua diferença em relação à Naive Bayes?

Se você já se aventurou no vasto campo da análise de dados e aprendizado de máquina, provavelmente se deparou com o dilema crucial de escolher o melhor algoritmo para o seu projeto. Dois contendores frequentes nessa batalha são as Árvores de Decisão e os Classificadores Naive Bayes. Ambos têm méritos distintos, mas discernir qual é mais adequado para sua aplicação específica pode ser desafiador. Neste post, mergulharemos nas características únicas de cada um, destacando suas vantagens, desvantagens e cenários ideais de uso. Vamos desvendar o mistério por trás da escolha entre Árvore de Decisão e Naive Bayes, guiando-o pelo caminho da decisão informada no mundo fascinante da análise preditiva.

# Importar bibliotecas
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import accuracy_score

# Passo 1: Carregar e selecionar os dados
iris = load_iris()
data = pd.DataFrame(data= np.c_[iris['data'], iris['target']], columns= iris['feature_names'] + ['target'])

# Passo 2: Dividir os dados em recursos (X) e rótulos (y)
X = data.drop('target', axis=1)
y = data['target']

# Passo 3: Dividir os dados em conjuntos de treinamento e teste
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Passo 4: Criar e treinar o modelo de árvore de decisão
model = DecisionTreeClassifier(random_state=42)
model.fit(X_train, y_train)

# Passo 5: Plotar a árvore de decisão
plt.figure(figsize=(12, 8))
plot_tree(model, feature_names=iris.feature_names, class_names=iris.target_names, filled=True, rounded=True)
plt.show()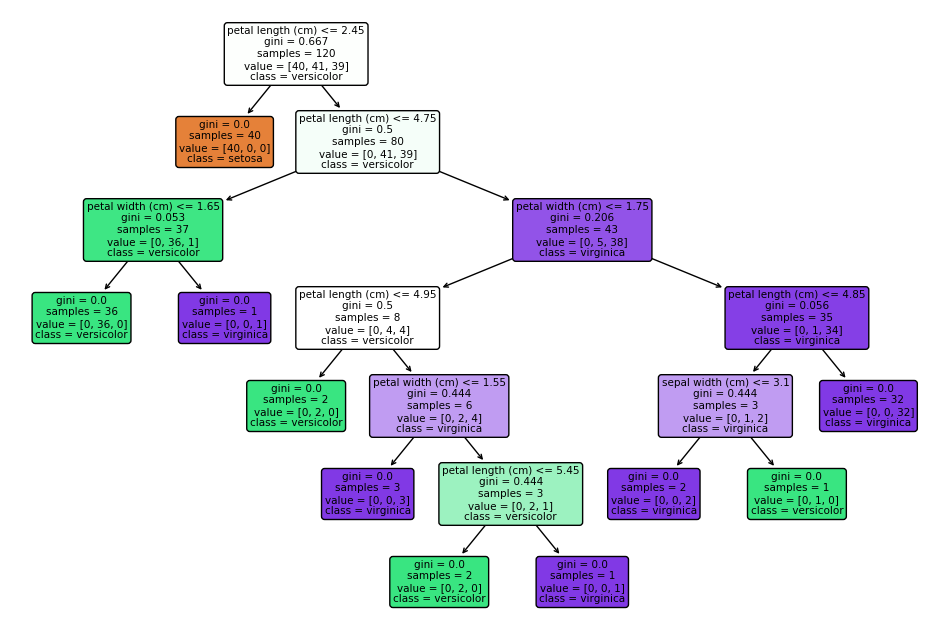

# Passo 6: Fazer previsões no conjunto de teste
y_pred = model.predict(X_test)

# Passo 7: Calcular a acurácia do modelo
accuracy = accuracy_score(y_test, y_pred)
print(f'Acurácia: {accuracy:.2f}')

# Passo 8: Plotar gráfico com os tipos de flor com base nos critérios
plt.figure(figsize=(10, 6))
for i, feature in enumerate(iris.feature_names):
    plt.subplot(2, 2, i+1)
    for target in iris.target_names:
        subset = data[data['target'] == iris.target_names.tolist().index(target)]
        plt.hist(subset[feature], bins=10, label=target, alpha=0.7)
    plt.xlabel(feature)
    plt.legend()
plt.tight_layout()
plt.show()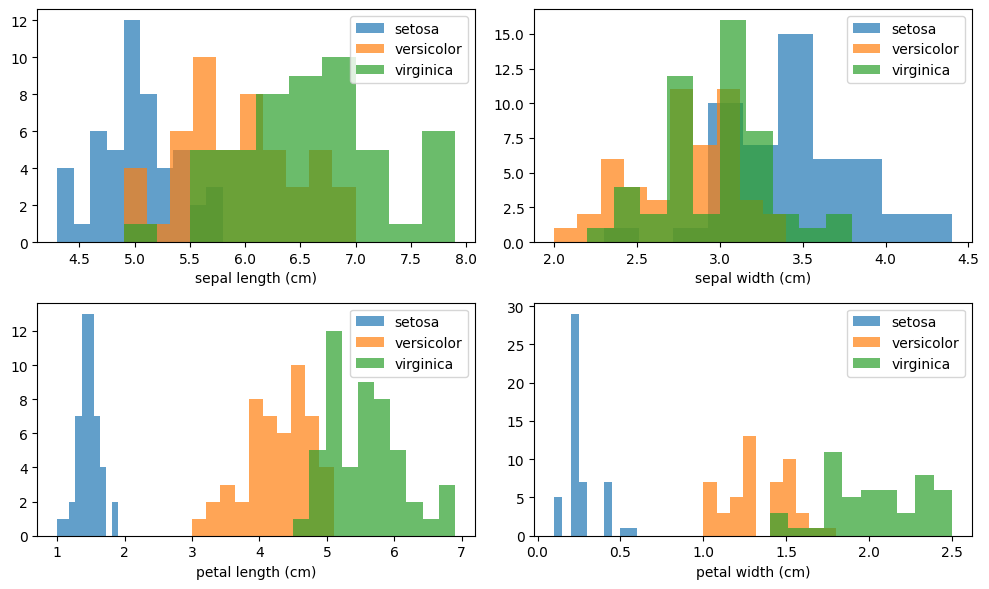

O gráfico gerado pelo código mostra quatro subgráficos, cada um representando a distribuição de uma característica (Comprimento da sépala, Largura da sépala, Comprimento da pétala, Largura da pétala) para cada uma das três classes de flores no conjunto de dados Iris (Setosa, Versicolor, Virginica).
Comprimento da Sépala (Subgráfico Superior Esquerdo):

O eixo x representa os valores de comprimento da sépala. Cada classe (Setosa, Versicolor, Virginica) tem sua própria distribuição, mostrada por diferentes cores ou padrões no histograma. A sobreposição entre as distribuições indica como as classes podem se sobrepor nessa característica. Largura da Sépala (Subgráfico Superior Direito):
Semelhante ao primeiro subgráfico, mas para a largura da sépala. Comprimento da Pétala (Subgráfico Inferior Esquerdo):
Exibe as distribuições para o comprimento da pétala. Largura da Pétala (Subgráfico Inferior Direito):
Mostra as distribuições para a largura da pétala.

Interpretação Geral:
A sobreposição ou separação clara entre as classes em cada subgráfico indica quão bem uma característica específica pode discriminar entre as diferentes classes. Se as distribuições para uma característica e classe específica são distintas, essa característica é potencialmente útil para classificação. Se houver sobreposição significativa, pode indicar que essa característica pode não ser tão discriminativa para aquela classe específica. Exemplo:
Se, por exemplo, no subgráfico de Comprimento da Sépala, a distribuição da classe Setosa estiver claramente separada das distribuições das outras classes, isso sugere que o comprimento da sépala é uma característica forte para distinguir a classe Setosa. Em resumo, a interpretação desses gráficos ajuda a entender como as diferentes classes se comportam em relação a cada característica, fornecendo insights valiosos sobre a relevância discriminativa de cada característica no processo de classificação.

# Criar uma lista para armazenar as acurácias
accuracies = []

# Testar diferentes números de árvores de decisão
for n_trees in range(1, 21):
    # Criar e treinar o modelo de árvore de decisão
    model = DecisionTreeClassifier(random_state=42, max_depth=n_trees)
    model.fit(X_train, y_train)

    # Fazer previsões no conjunto de teste
    y_pred = model.predict(X_test)

    # Calcular a acurácia do modelo
    accuracy = accuracy_score(y_test, y_pred)
    accuracies.append(accuracy)

# Plotar o gráfico de acurácia em relação ao número de árvores de decisão
plt.figure(figsize=(10, 6))
plt.plot(range(1, 21), accuracies, marker='o', linestyle='-', color='b')
plt.title('Acurácia do Modelo em Relação ao Número de Árvores de Decisão')
plt.xlabel('Número de Árvores de Decisão')
plt.ylabel('Acurácia')
plt.grid(True)
plt.show()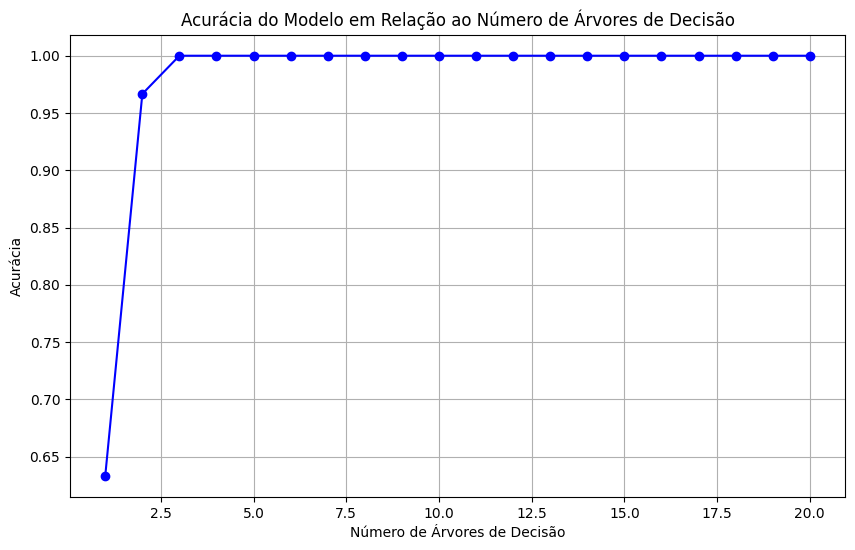

Pensando em uma árvore de forma literal, ela é composta por galhos e folhas. Se tratando de algoritmos, cada galho é uma pergunta e cada folha é uma resposta. Nesse contexto, a árvore de decisão divide os dados em diferentes grupos com base em características específicas. Essa ramificação é realizada por meio de uma série de perguntas sequenciais, as quais filtram os dados progressivamente até alcançar uma conclusão. O processo de tomada de decisão se desenrola de forma hierárquica, onde cada pergunta subsequente visa refinar e direcionar os dados para segmentos mais específicos.

Por outro lado, o algoritmo Naive Bayes é fundamentado em um princípio estatístico. Sua abordagem se baseia na avaliação de probabilidades para prever a ocorrência de eventos futuros, utilizando como base as probabilidades de eventos anteriores. Este algoritmo opera sob a suposição de independência entre os eventos, ou seja, considera que cada evento é independente dos demais, dado o resultado a ser previsto.

Partindo para a prática, é possível compreender que, ao treinar sua floresta de árvores de decisão com um número relativamente baixo, como 2,5 árvores, a acurácia do modelo pode atingir 1. Isso sugere que o modelo está se ajustando excessivamente aos dados de treinamento, memorizando padrões específicos em vez de generalizar para novos dados. É fundamental avaliar o desempenho do modelo em conjuntos de teste independentes para garantir uma boa generalização e evitar overfitting.

from sklearn.naive_bayes import GaussianNB
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt


nb_model = GaussianNB()
dt_model = DecisionTreeClassifier(random_state=42)

# Treinar os modelos
nb_model.fit(X_train, y_train)
dt_model.fit(X_train, y_train)

# Fazer previsões nos conjuntos de teste
y_pred_nb = nb_model.predict(X_test)
y_pred_dt = dt_model.predict(X_test)

# Calcular acurácias
accuracy_nb = accuracy_score(y_test, y_pred_nb)
accuracy_dt = accuracy_score(y_test, y_pred_dt)

# Plotar o gráfico comparativo de acurácia
labels = ['Naive Bayes', 'Decision Tree']
accuracies = [accuracy_nb, accuracy_dt]

plt.bar(labels, accuracies, color=['blue', 'green'])
plt.ylim(0.0, 1.0)  # Ajuste o limite do eixo y de 0 a 1 para representar a porcentagem
plt.ylabel('Acurácia')
plt.title('Comparação de Acurácia entre Naive Bayes e Árvore de Decisão')
plt.show()

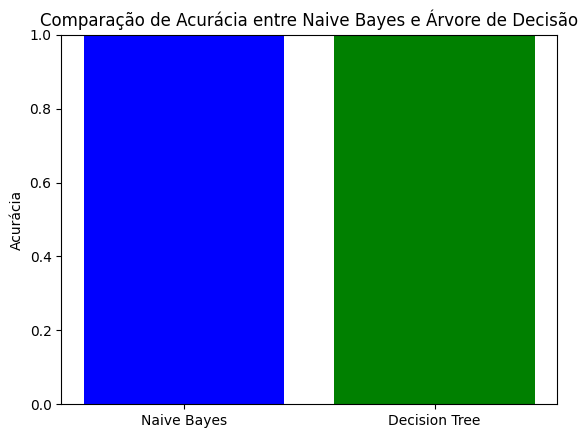
No âmbito desta análise comparativa entre os modelos de classificação Naive Bayes e Árvore de Decisão, os resultados obtidos sugerem uma equivalência notável em termos de acurácia. A acurácia, embora uma métrica comum, pode não ser suficiente para uma avaliação abrangente do desempenho, especialmente em casos de desbalanceamento de classes.

from sklearn.model_selection import cross_val_score

# Criar uma lista para armazenar as acurácias
accuracies = []

# Testar diferentes números de árvores de decisão
for n_trees in range(1, 21):
    # Criar e treinar o modelo de árvore de decisão
    model = DecisionTreeClassifier(random_state=42, max_depth=n_trees)

    # Realizar validação cruzada
    cv_scores = cross_val_score(model, X_train, y_train, cv=5)  # 5-fold cross-validation
    mean_accuracy = np.mean(cv_scores)
    accuracies.append(mean_accuracy)

# Plotar o gráfico de acurácia em relação ao número de árvores de decisão
plt.figure(figsize=(10, 6))
plt.errorbar(range(1, 21), accuracies, marker='o', linestyle='-', color='b', yerr=np.std(cv_scores), label='Acurácia média ± Desvio Padrão')
plt.title('Acurácia Média do Modelo com Validação Cruzada em Relação ao Número de Árvores de Decisão')
plt.xlabel('Número de Árvores de Decisão')
plt.ylabel('Acurácia Média')
plt.legend()
plt.grid(True)
plt.show(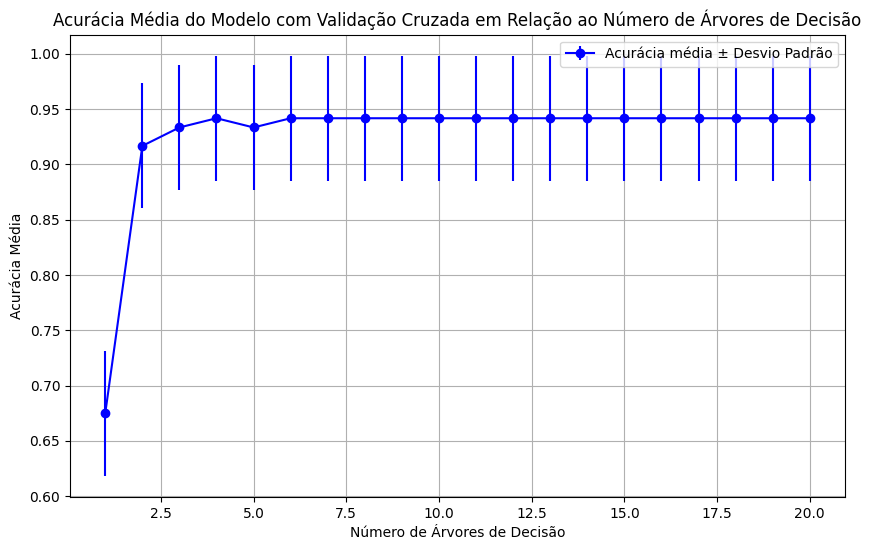

A validação cruzada, que consiste em dividir o conjunto de treinamento em subconjuntos para treinamento e teste em várias iterações, proporcionou uma visão mais abrangente do desempenho do modelo de Árvore de Decisão. A acurácia média, exibida graficamente em relação ao número de árvores, atingiu seu ponto máximo em aproximadamente 0.95 a partir de 6 árvores. Esse comportamento sugere que, ao adicionar mais árvores, o modelo inicialmente melhora, mas atinge um ponto de saturação onde a complexidade adicional não resulta em ganhos significativos de desempenho.

from sklearn.metrics import precision_score

# Calcular a precisão para Naive Bayes
precision_nb = precision_score(y_test, y_pred_nb, average='weighted')

# Calcular a precisão para Árvore de Decisão
precision_dt = precision_score(y_test, y_pred_dt, average='weighted')

# Exibir os resultados
print(f'Precisão (Naive Bayes): {precision_nb:.4f}')
print(f'Precisão (Árvore de Decisão): {precision_dt:.4f}')

Precisão (Naive Bayes): 1.0000
Precisão (Árvore de Decisão): 1.0000

from sklearn.metrics import recall_score

# Calcular a revocação para Naive Bayes
recall_nb = recall_score(y_test, y_pred_nb, average='weighted')

# Calcular a revocação para Árvore de Decisão
recall_dt = recall_score(y_test, y_pred_dt, average='weighted')

# Exibir os resultados
print(f'Revocação (Naive Bayes): {recall_nb:.4f}')
print(f'Revocação (Árvore de Decisão): {recall_dt:.4f}')

Neste contexto, outras métricas foram consideradas para enriquecer a análise. A precisão e a revocação foram calculadas para cada modelo, proporcionando uma visão mais aprofundada das capacidades de discriminação e identificação de instâncias positivas. A precisão destaca a proporção de verdadeiros positivos em relação a todos os exemplos classificados como positivos, enquanto a revocação representa a proporção de verdadeiros positivos em relação a todos os exemplos verdadeiramente positivos.

Ao analisar os resultados obtidos através dos diferentes métodos de avaliação, observamos que a acurácia para ambos os modelos, Naive Bayes e Árvore de Decisão, atingiu o valor máximo de 1.0 nos conjuntos de teste. Essa elevada precisão inicial pode levantar suspeitas de overfitting, especialmente ao considerar a complexidade dos modelos e a possibilidade de memorização dos dados de treinamento.

A avaliação da precisão, uma métrica que leva em conta tanto os verdadeiros positivos quanto os falsos positivos e negativos, também revelou valores perfeitos de 1.0 para ambas as abordagens. Embora esses resultados possam inicialmente sugerir um desempenho excepcional, é crucial interpretá-los com cautela, especialmente quando se trata de generalização para dados não vistos.

Portanto, diante desses resultados, é recomendável considerar uma análise mais aprofundada, explorando possíveis ajustes nos parâmetros dos modelos ou considerando outras métricas de avaliação, além de verificar a capacidade de generalização em conjuntos de teste independentes. Este processo visa garantir robustez e confiabilidade na aplicação dos modelos em cenários do mundo real.

import matplotlib.pyplot as plt
import time
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.tree import DecisionTreeClassifier

# Carregar conjunto de dados Iris
iris = load_iris()
X = iris.data
y = iris.target

# Dividir os dados em conjunto de treinamento e teste
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Inicializar os modelos
nb_model = GaussianNB()
dt_model = DecisionTreeClassifier(random_state=42)

# Medir o tempo de processamento para o Naive Bayes
start_time_nb = time.time()
nb_model.fit(X_train, y_train)
end_time_nb = time.time()
time_nb = end_time_nb - start_time_nb

# Medir o tempo de processamento para a árvore de decisão
start_time_dt = time.time()
dt_model.fit(X_train, y_train)
end_time_dt = time.time()
time_dt = end_time_dt - start_time_dt

# Plotar o gráfico comparativo de tempo de processamento
labels = ['Naive Bayes', 'Decision Tree']
times = [time_nb, time_dt]

plt.bar(labels, times, color=['blue', 'green'])
plt.ylabel('Tempo de Processamento (s)')
plt.title('Comparação de Tempo de Processamento entre Naive Bayes e Árvore de Decisão')
plt.show()

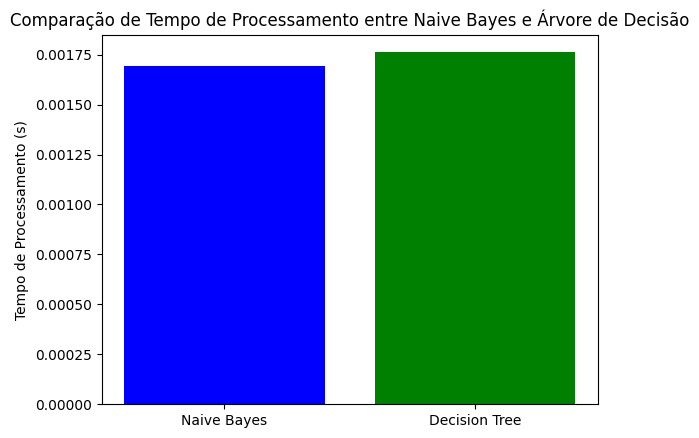
A análise comparativa do tempo de processamento entre o modelo Naive Bayes e a Árvore de Decisão revela resultados interessantes. Ao examinar o gráfico, observamos que o tempo de processamento para a Árvore de Decisão é ligeiramente superior ao do Naive Bayes, embora ambos estejam na ordem de magnitude de 0.00175 segundos.

Este pequeno diferencial pode ser atribuído às características intrínsecas dos algoritmos. O Naive Bayes é conhecido por sua eficiência computacional, especialmente em conjuntos de dados menores, devido à sua abordagem probabilística simples. Por outro lado, a Árvore de Decisão, ao envolver a construção de uma estrutura hierárquica de decisões, pode demandar um pouco mais de tempo computacional.

É essencial notar que, apesar da diferença observada, ambos os tempos de processamento são extremamente baixos, indicando que tanto o Naive Bayes quanto a Árvore de Decisão são algoritmos eficientes para o conjunto de dados Iris utilizado. A escolha entre esses modelos pode depender não apenas do tempo de processamento, mas também de outros fatores, como interpretabilidade do modelo, desempenho em diferentes tipos de dados e a natureza específica do problema em questão.

Autores

Catarina Lima Mendes (172787)

Lais Azevedo Soares (173455 )

Laryssa Oliveira Silva (173501)

Luisa Martins Felix De Oliveira (173648)

Natalia Emboava (173709)