Introdução a Regressão

A regressão é uma técnica estatística que busca modelar e definir a relação entre uma variável dependente (resposta) e uma ou mais variáveis independentes (preditoras). O objetivo é entender como as mudanças nas variáveis independentes estão associadas a mudanças na variável dependente.

Podemos usar essa técnica para “prever” valores futuros da variável resposta com base em supostos valores para as preditoras, ou para inferir relações entre a variável resposta e suas dependentes. Observe a explicação:

Diferença entre Regressão por Inferência e Regressão por Previsão/Predição

Regressão por Inferência

  • Foca em entender relações entre variáveis.
  • Busca identificar quais variáveis são estatisticamente significativas para explicar a variabilidade na variável dependente.
  • Utiliza testes de hipóteses e intervalos de confiança para inferências.

Como exemplo prático, podemos imaginar uma avaliação de como diferentes fatores influenciam o preço de uma casa.

Regressão por Previsão/Predição

  • Foca na capacidade do modelo de fazer previsões precisas.
  • Menor ênfase na interpretação detalhada dos coeficientes.
  • Importância na seleção de modelos com boa capacidade preditiva.

Como exemplo prático, podemos tentar prever o preço futuro de uma casa com base em características como número de quartos, localização, etc.

Objetivo da Regressão por Inferência

Entender a Relação entre Variáveis

O principal objetivo da regressão por inferência é compreender como as variáveis independentes estão relacionadas à variável dependente. Busca-se identificar e quantificar o impacto de cada variável na variável de interesse.

Ao contrário da regressão por previsão, onde o foco é criar um modelo que faça previsões precisas, na regressão por inferência, o interesse vai além das previsões. A ênfase está na explicação do relacionamento subjacente entre as variáveis, mesmo que isso signifique sacrificar um pouco a precisão preditiva.

Interpretabilidade dos Coeficientes

Na regressão por inferência, a interpretabilidade dos coeficientes desempenha um papel crucial. Cada coeficiente está relacionado a uma variável independente e indica a alteração média na variável dependente, que ocorre quando a variável independente associada aumenta em uma unidade, mantendo todas as outras variáveis constantes.

Essa interpretabilidade é valiosa para entender o impacto prático das variáveis e comunicar resultados a não-especialistas.


Por exemplo: Se o coeficiente associado à variável “quantidade de quartos” de uma casa for 0,20, isso pode ser interpretado como um aumento médio de 0,20 unidades na variável dependente para cada quarto adicional.

Aprofundamento na Causalidade

A regressão por inferência permite uma abordagem mais aprofundada na busca por relações causais entre as variáveis. Embora não prove causalidade definitiva, a interpretação cuidadosa dos coeficientes pode ajudar a formular hipóteses sobre a direção da causalidade.

Modelo de Regressão Linear

Forma Geral do Modelo de Regressão Linear

Um modelo de regressão linear simples é dado por:

y = β0 + β1×1 + e

Este modelo será explorado nestes exemplos iniciais. Mais à frente, abordaremos o modelo de Regressão Linear Múltipla, dado por:

y = β0 + β1×1 + β2×2 + … + βnxn + e

Nesses modelos:

y : é a variável resposta (dependente)

xi : é a variável preditora (independente)

β0 : é o intercepto ou coeficiente linear, representando o valor esperado de Y quando todas as variáveis independentes são zero.

β1 : é o coeficiente angular ou de regressão. São os coeficientes associados a cada variável independente, indicando a mudança média em Y para uma unidade de mudança na respectiva variável independente, mantendo todas as outras constantes.

e : é o termo de erro, representando a variação não explicada no modelo

Interpretação dos termos fundamentais

Intercepto (βo):

Representa o valor de Y quando todas as variáveis independentes são zero. Em alguns contextos, pode ter significado prático; em outros, pode não ter interpretação real, dependendo do domínio do problema (será demonstrado no exemplo à seguir).

Coeficientes (β1, β2…):

Indicam a mudança média em Y associada a uma unidade de mudança na variável independente correspondente. Interpretar esses coeficientes é crucial para entender a influência relativa das variáveis no resultado.

Termo de erro (e):

Captura a variação em Y que não é explicada pelas variáveis independentes incluídas no modelo. Reflete a presença de fatores não observados ou aleatórios que afetam Y.

Exemplo

Consideremos um modelo de regressão linear que tenta prever o preço de casas (Y) com base no tamanho da casa (X1).

Segundo a fórmula y = β0 + β1×1 + e, teríamos:

Preço = β0 + β1 (tamanho) + e.

Neste caso, β0 representaria o preço esperado quando o tamanho da casa e o número de quartos são zero, o que não tem um significado prático real.

β1 indicaria a mudança média no preço para uma unidade de aumento no tamanho da casa, mantendo o número de quartos constante.

β2 indicaria a mudança média no preço para uma unidade de aumento no número de quartos, mantendo o tamanho da casa constante.

Pressupostos da Regressão

Alguns conceitos que são de importante conhecimento antes de aprendemos sobre regressão, são

Linearidade

O pressuposto de linearidade assume que a relação entre as variáveis independentes e a variável dependente é linear. Isso significa que as mudanças nas variáveis independentes estão associadas a mudanças proporcionais na variável dependente.

A violação desse pressuposto pode levar a estimativas enviesadas e imprecisas dos coeficientes de regressão.

Independência dos Erros

Os erros do modelo devem ser independentes entre si. Isso significa que o valor de erro associado a uma observação não deve depender dos valores de erro de outras observações.

A violação desse pressuposto pode levar a padrões sistemáticos nos resíduos, comprometendo a validade das inferências estatísticas.

Homocedasticidade

A variabilidade dos erros deve ser constante em todos os níveis das variáveis independentes. Isso implica que a dispersão dos resíduos não deve depender dos valores previstos pelo modelo.

A heterocedasticidade (variabilidade desigual dos resíduos) pode afetar a eficiência dos estimadores e distorcer os intervalos de confiança.

Normalidade dos Erros

Assume-se que os erros do modelo se distribuem normalmente. Isso não significa que as variáveis observadas precisam ser normalmente distribuídas, mas sim que os erros do modelo (resíduos) devem seguir uma distribuição normal.

A normalidade dos erros é fundamental para realizar inferências estatísticas, como intervalos de confiança e testes de hipóteses. Em grandes amostras, a normalidade dos erros pode ser menos crítica devido ao Teorema Central do Limite.

Independência entre Variáveis Independentes

As variáveis independentes devem ser independentes entre si, evitando multicolinearidade perfeita, onde uma variável pode ser prevista com precisão a partir de outras variáveis independentes.

A multicolinearidade pode levar a estimativas imprecisas dos coeficientes e dificultar a interpretação do impacto individual das variáveis.

Ausência de Erros de Medição

Assume-se que as variáveis medidas são livres de erros. Erros de medição podem distorcer as relações reais entre as variáveis.

Erros de medição podem levar a conclusões incorretas sobre as relações entre variáveis, afetando a validade do modelo.

Exemplo Prático de Inferência

Após uma boa introdução teórica, vamos ver um exemplo básico de inferência.

Usaremos Python para nos ajudar a extrair dados de uma banco com informações sobre “SATs” e “GPAs” de alunos estadunidenses.

Mais informações serão fornecidas ao longo do exemplo.

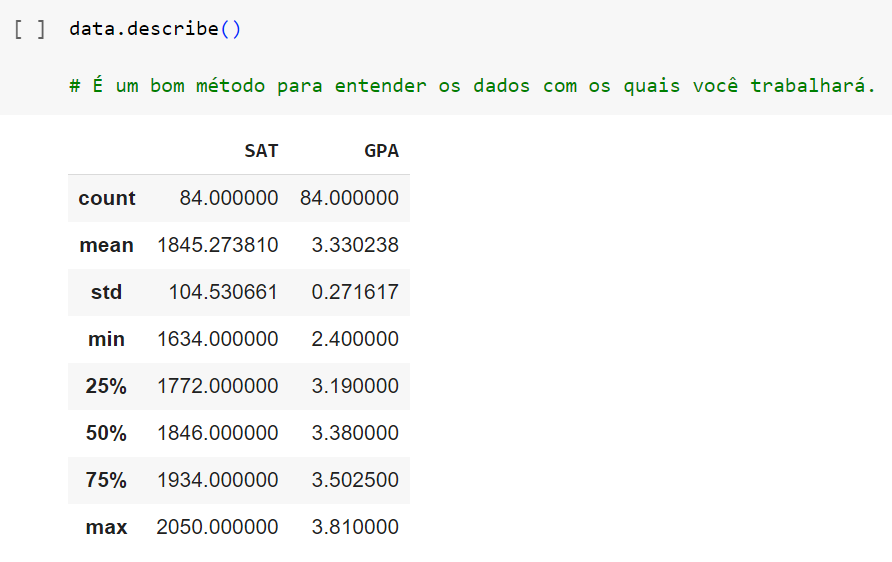
É sempre importante, ao criarmos um modelo de regressão, que ele seja significativo.

Pense, por que tentaríamos prever o GPA de um aluno com base no seu SAT? Ou, no caso da inferência, por que uma dessas variáveis impactaria na próxima?

O SAT é uma prova também usada para avaliar alunos americanos.

A prova tem uma parte de interpretação de texto e uma parte de matemática, obrigatoriamente. Além disso, o aluno pode optar por fazer sem redação ou com redação

O GPA (Grade Point Average) é o formato que os Estados Unidos calculam a média das notas do aluno nos quatro últimos anos de escola.

Desse modo, é esperado que alunos com maior GPA se saiam melhor em seus SATs. Igualmente, é esperado que alunos que se saiam bem em seus SATs tenham altos GPAs.

Considerando a fórmula que vimos, y = b0 + b1x1, vamos formar o código:

Observando o gráfico a olho-nu, já fica claro que há uma relação clara entre SAT e GPA. No geral, quanto maior o SAT, mais alto tende a ser o GPA. Com essa informação clara, vamos para a regressão em si:

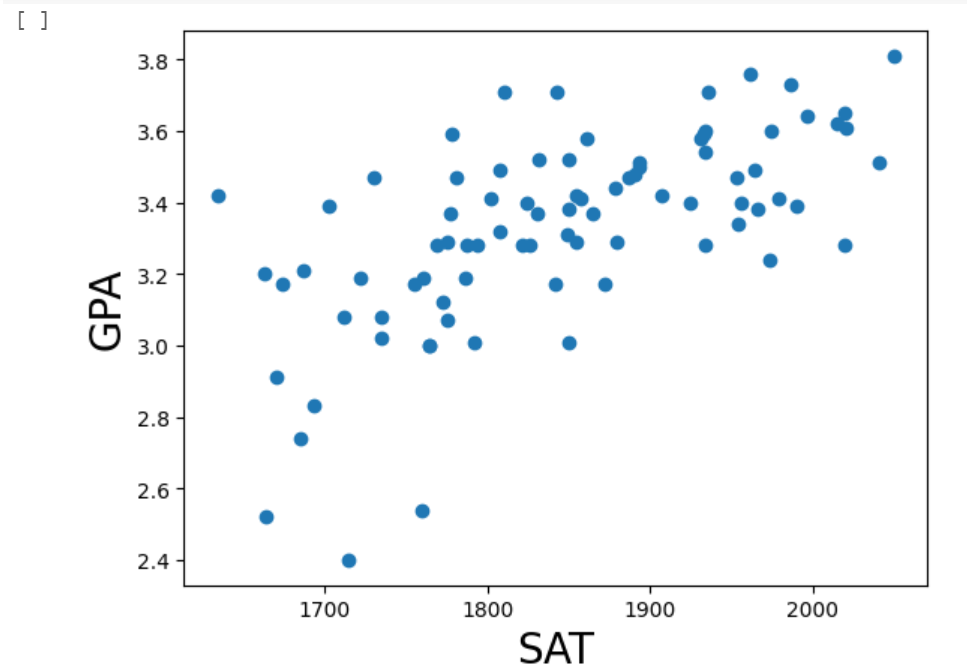
Antes de vermos o código em si, precisamos entender uma questão:

Para definir a regressão, vamos criar uma variável X. Na fórmula de regressão y = b0 + x1b1, observamos que b0 não possui coeficiente, então, de onde vem x?

Entenda: o coeficiente b0 também pode ser representado como b0 * 1. Esse valor 1, no caso, seria o coeficiente x0. Tal coeficiente é retirado da fórmula, pois seu valor seria sempre igual a um.

Apesar disso, para propósitos computacionais, é bastante interessante incorporar essa noção à equação. Observe:

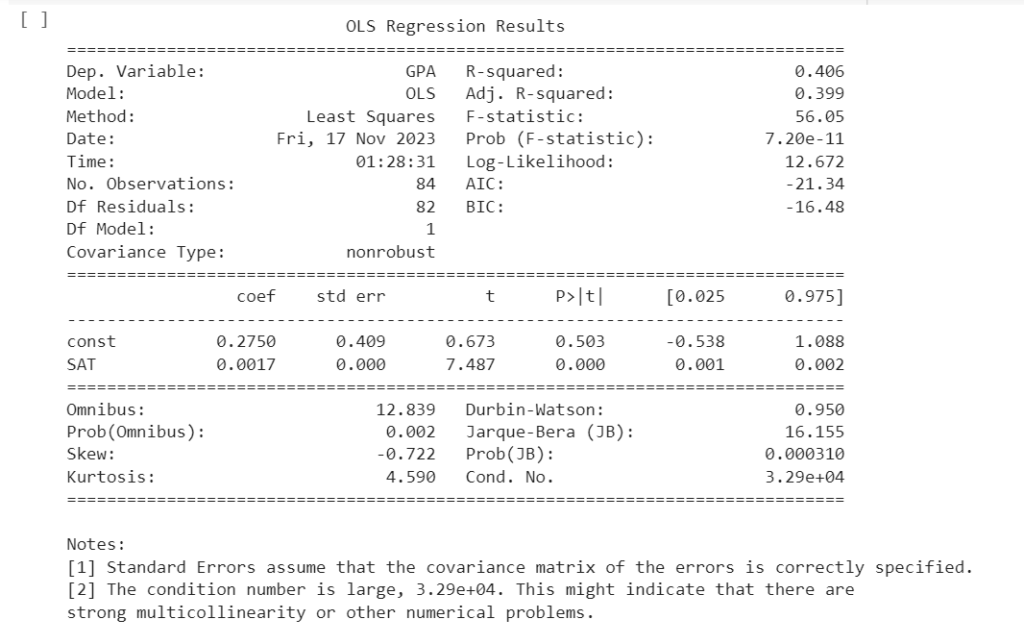
Usaremos os dados obtidos acima para desenhar a “best fitting line” ou linha de melhor ajuste. Observe:

Teste de Hipóteses e Intervalo de Confiança

Apesar de, a olho-nu e “logicamente”, a relação entre as variáveis ser clara, introduziremos um conceito final nesse exemplo, que é essencial à Inferência Estatística: o Teste de Hipóteses.

Às vezes, é possível que estatísticas “aparentemente” relacionadas não estejam relacionadas o suficiente para comprovarem o que queremos. Ou, podemos ter viéses, e querermos que dois atributos estejam relacionados. Nesses casos, usamos o teste de hipóteses.

Um teste de hipóteses é uma ferramenta estatística usada para tomar decisões sobre as populações com base nas amostras. Ele está diretamente associado ao intervalo de confiança.

Um intervalo de confiança é uma faixa de valores na qual acredita-se que um parâmetro (como um coeficiente de regressão) esteja com uma certa probabilidade.

Por exemplo, um intervalo de confiança de 95% indica que, se repetíssemos a amostragem muitas vezes, o verdadeiro valor do coeficiente estaria dentro desse intervalo em 95% das vezes.

No contexto de regressão, um teste de hipóteses permite avaliar se os coeficientes estimados são estatisticamente significativos. Geralmente, essa avaliação é feita com um intervalo de confiança de 95%.

Um p-valor associado ao teste indica a probabilidade de observar os resultados observados (ou mais extremos) se a hipótese nula de que o coeficiente é zero for verdadeira.

A avaliação da significância estatística ajuda na tomada de decisões sobre quais variáveis incluir ou excluir do modelo. Variáveis estatisticamente insignificantes podem ser removidas, simplificando o modelo sem comprometer sua capacidade explicativa.

Ao realizar o teste de hipóteses, obtemos um p-valor associado ao coeficiente do tamanho da casa. Se o p-valor (100% – intervalo de confiança) for suficientemente baixo, podemos rejeitar a hipótese nula.

Observemos no código abaixo um exemplo:

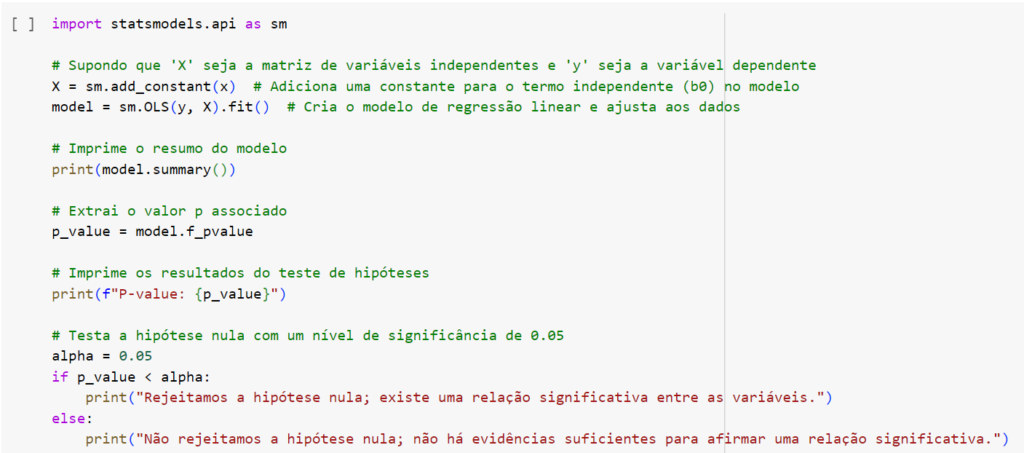
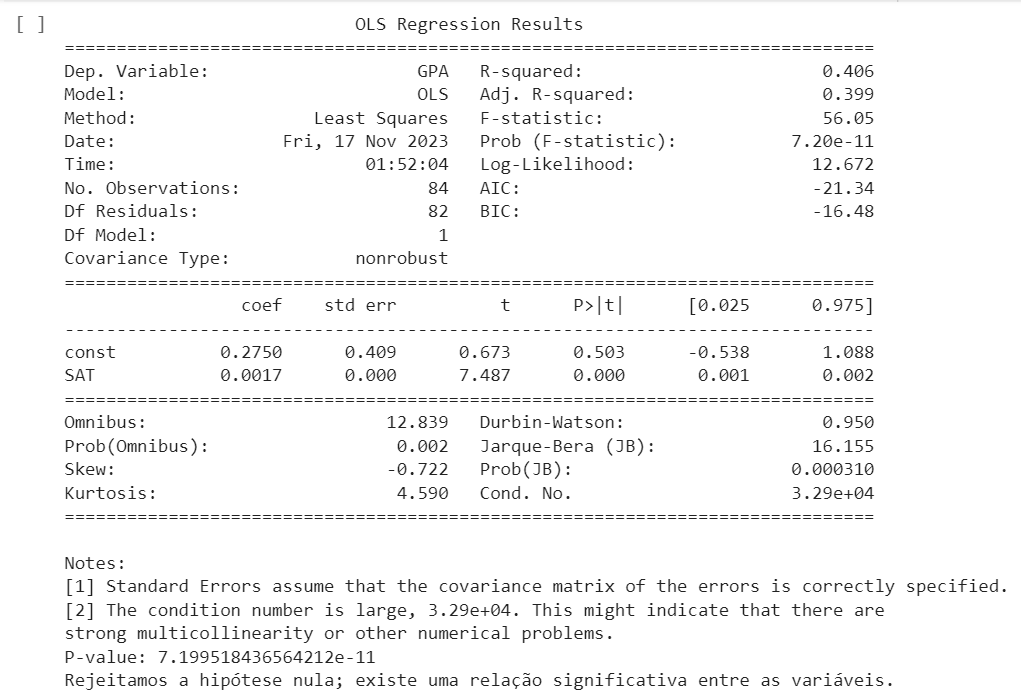
Parabéns! Neste exemplo, criamos nosso primeiro algoritmo de Regressão Linear, e pudemos inferir uma relação a partir dele.

Modelos de Regressão Linear e Inferência

É bastante fácil fazermos inferências em modelos de regressão simples. Se o modelo estiver correto, com um bom nível de confiabilidade, as variáveis se influenciam diretamente.

Para estes exemplos a seguir, continuaremos com códigos em Python. Como o foco é a Regressão e a Inferência, e não o código em si, explicaremos o que cada código faz o como interpretar os resultados.

Para vermos um exemplo mais real, escolhemos um modelo que discute a performance de alunos no Ensino Médio. Essa base de dados pode ser acessada aqui.

Esse dataset é bastante útil para tarefas de predições e inferência usando diversos algoritmos.

Para hoje, iremos explorar os dados, inferirindo mais relações entre variáveis. Com essa base de dados, poderemos exemplificar conceitos essenciais à Inferência, como métricas de avaliação, Variáveis Dummy e Multicolinearidade.

Os dados desse banco incluem notas dos alunos, questões demográficas e sócio-econômicas, e foram coletadas por meio de questionários nas escolas.

Análise Exploratória de Dados, ou EDA (Exploratory Data Analysis)

Obtendo um banco de dados maior e mais complexo, precisamos, primeiro, entender os dados e sobre o que se tratam.

A análise exploratória de dados é uma abordagem fundamental na área da ciência de dados. Ela envolve a exploração e o entendimento dos dados. Aqui, buscamos compreender os dados que estamos analisando, e identificar possíveis correlações.

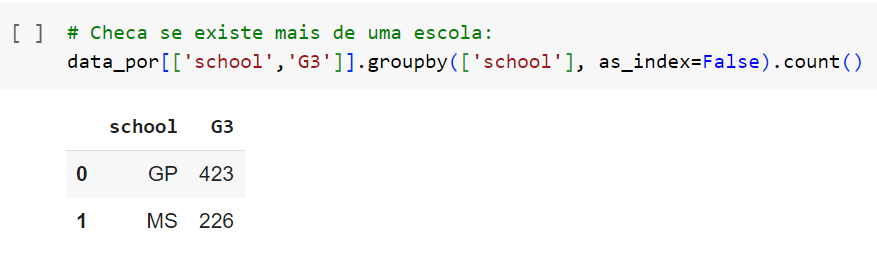
Identificamos que 423 alunos pertencem a “GP” e 226 a “MS”. Observe no gráfico abaixo:

Ainda assim, é importante que nosso modelo sirva para alunos de ambas as escolas.

Inferências

Com os dados pré-analisados, temos uma noção básica de que tipo de informações estamos vendo. Agora, podemos partir para inferências. Algumas questões que talvez sejam interessantes sabermos são:

  1. Alunos mais velhos tendem a terem melhores ou piores notas?
  2. O tamanho da família do aluno tem alguma influência em suas notas?
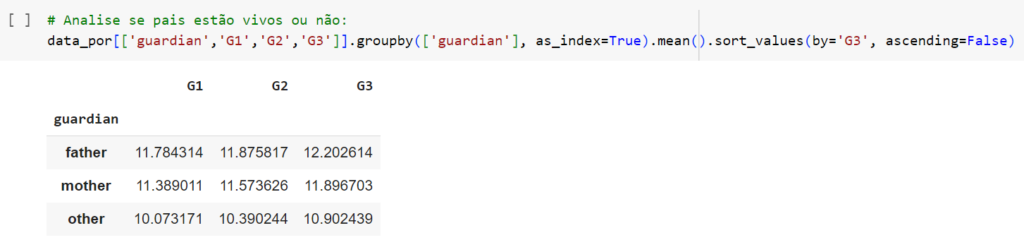
  3. Os empregos dos pais do aluno tem alguma influência em suas notas?
  4. O tempo que um aluno estuda tem alguma influência em suas notas?
  5. A escola do aluno importa?
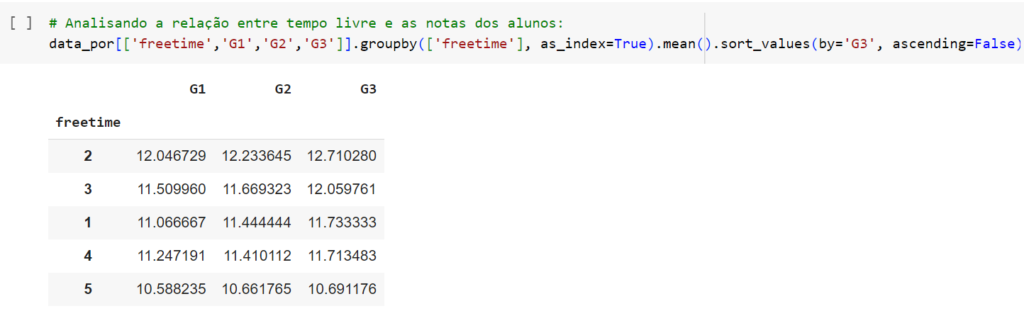
  6. Mais tempo livre resultou em notas melhores ou piores?

Para testar essas inferências, criaremos uma base data_corr, que copia os exatos dados de nossa base atual, para que possamos manipulá-la, sem alterar a base original. Nela, avaliaremos a correlação entre algumas variáveis.

A correlação varia de -1 a 1, onde:

  • 1 indica uma correlação perfeita positiva (quando uma variável aumenta, a outra também aumenta de maneira linear).
  • -1 indica uma correlação perfeita negativa (quando uma variável aumenta, a outra diminui de maneira linear).
  • 0 indica nenhuma correlação linear.

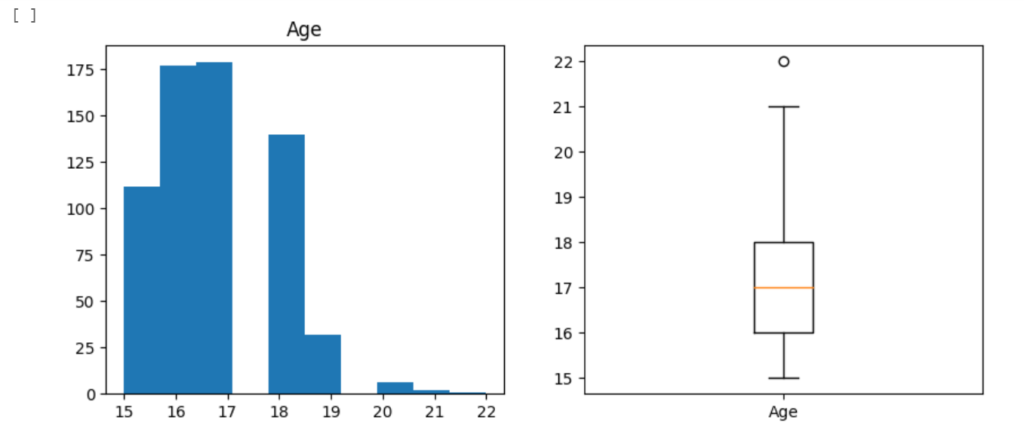
Vemos que a maioria dos alunos estão entre 15 a 19 anos, uma idade normal para alunos de Ensino Médio. Temos, aparentemente, um outlier de 22 anos, e alguns alunos entre 20 a 21 anos. Isso seria plausível, pensando que são, provavelmente, alunos que repetiram de ano.

A correlação é negativa, e bastante fraca. Isso não é surpreendente, se pensarmos que é provável que alunos de 20+ anos foram retidos por terem notas ruins.

Entenda a distribuiçao

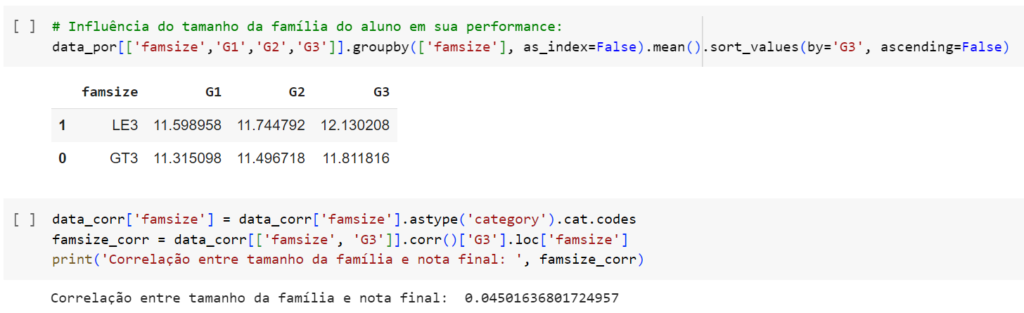
LE3: “Less than 3”. No caso, menos que 3. Alunos com uma família com menos de 3 membros parecem ter notas levemente maiores que alunos com famílias com mais de 3 membros.

Com essa análise, fica claro que alunos com pais no campo da educação e saúde tendem a ter melhores notas.
Alunos com pais vivos tendem a ter melhores notas
Entenda a representação:
 
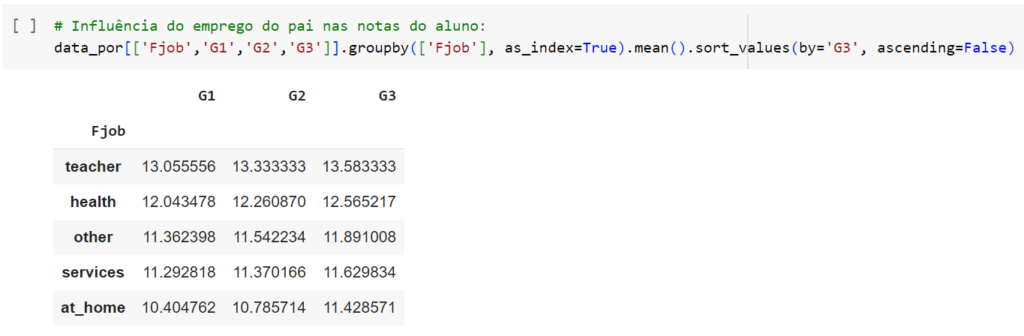
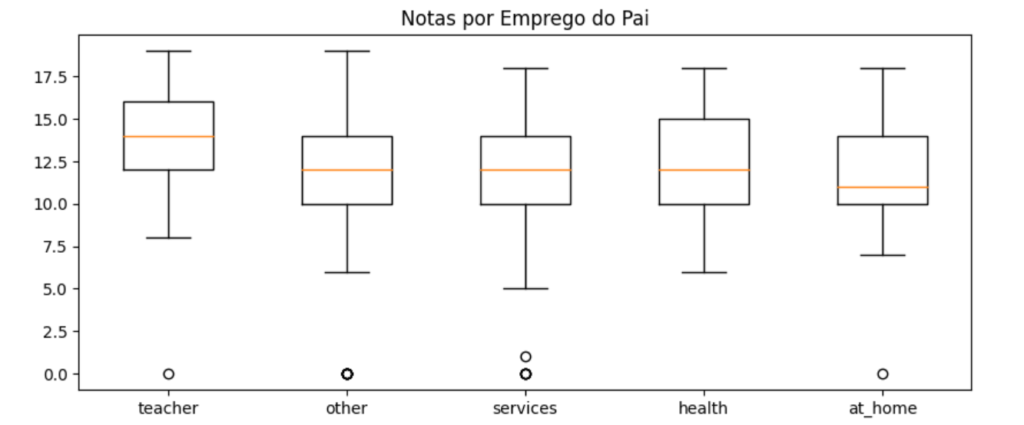
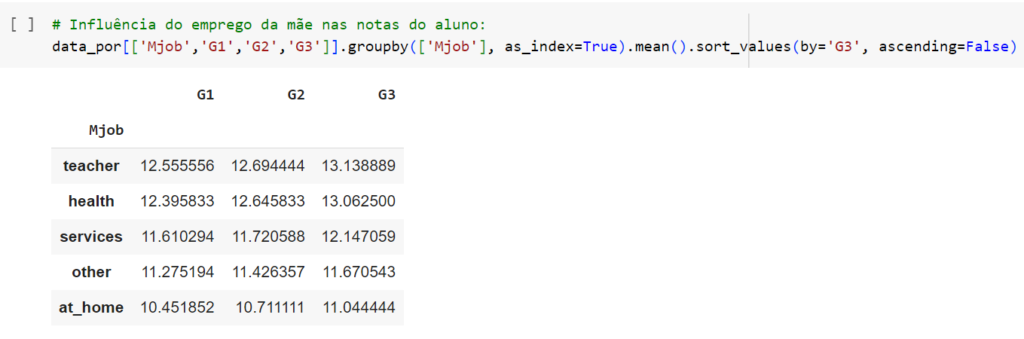
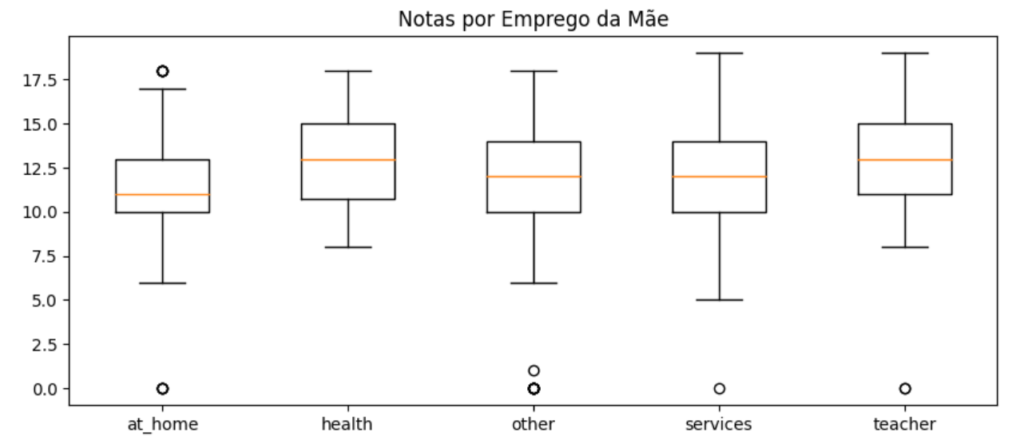
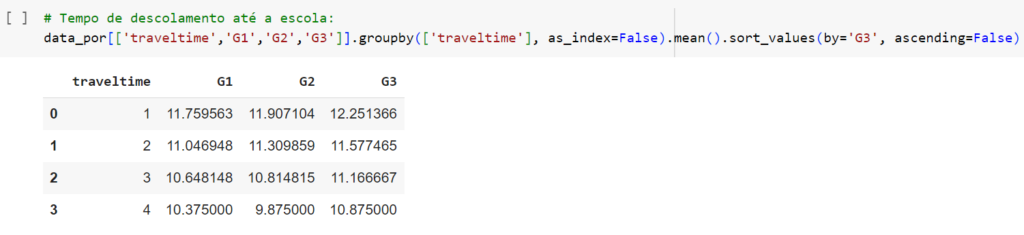
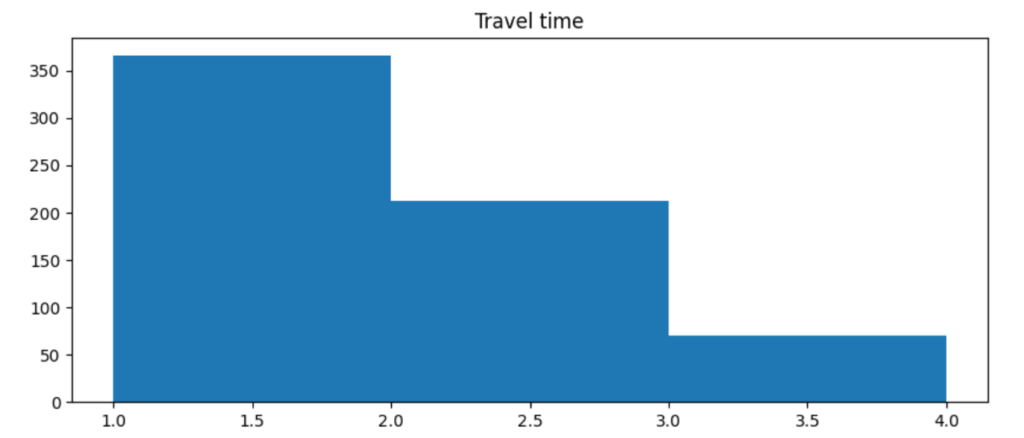
  • 1: Menos de 15 minutos
  • 2: Entre 15 minutos e 30 min
  • 3: Entre 30 minutos a 1 hora
  • 4: Mais que 1 hora
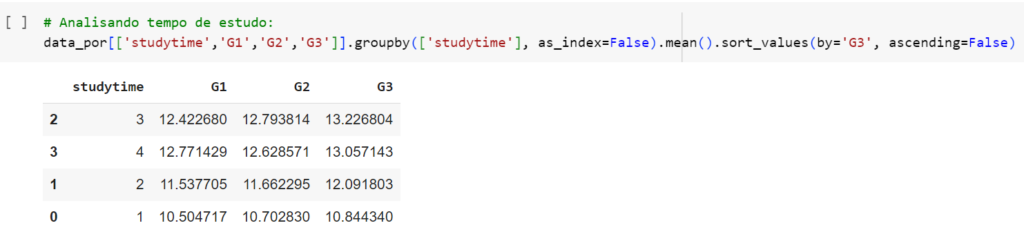
Fica claro que alunos que precisam se deslocar por menos tempo até a escola tem maiores notas.
Entenda a representação:
 
  • 1: Menos de 2 horas
  • 2: Entre 2 horas e 5 horas
  • 3: Entre 5 horas e 10 horas
  • 4: Mais que 10 hr
É esperado que a correlação entre esses atributos seja maior. Observe:

Essa correlação ainda é bastante fraca. Isso pode significar, por exemplo, que alguns alunos mentiram nas respostas.

Há, seguramente, um viés por parte dos alunos em que pessoas alheias acreditem que passam diversas horas estudando.

Entenda a representação:
 
Dados numéricos, ordenados de 1 – muito baixo a 5 – altíssimo.

Alunos que consomem menos álcool tem melhores notas.
Com essa análise, é aparente que alunos com horas medianas de tempo livre possuem notas melhores que os que tem muitas horas de tempo livre (4 a 5) ou poucas (1 ou menos).

Por que analisar essas correlações?

Além de serem boas métricas para analisar a qualidade das inferências feitas, temos que entender uma questão: em bases de dados grandes como essa que estamos analisando, é difícil que todos os atributos tenham impactos reais no atributo que queremos prever.

Atributos como, por exemplo, a quantidade de tempo livre dos alunos e a quantidade de tempo que veem a amigos, provavelmente estão altamente correlacionados. Ou, atributos como gênero dos alunos e suas notas finais, provavelmente não estão correlacionados.

Analisar essas correlações nos ajuda a:

  1. Identificar de Relacionamentos Lineares, ajudando a perceber padrões nos dados e entender como as variáveis estão relacionadas.

  2. Selecionar Variáveis para Modelagem, contribuindo para um modelo mais simples e interpretação mais fácil.

  3. Identificar Multicolinearidade (será explicado adiante).

Gráficos de dispersão associados à análise de correlação podem proporcionar uma visualização direta dos padrões nos dados. Isso pode ajudar a identificar tendências, outliers e padrões não lineares. Observe, abaixo, o gráfico de correlação dos atributos que possuímos:

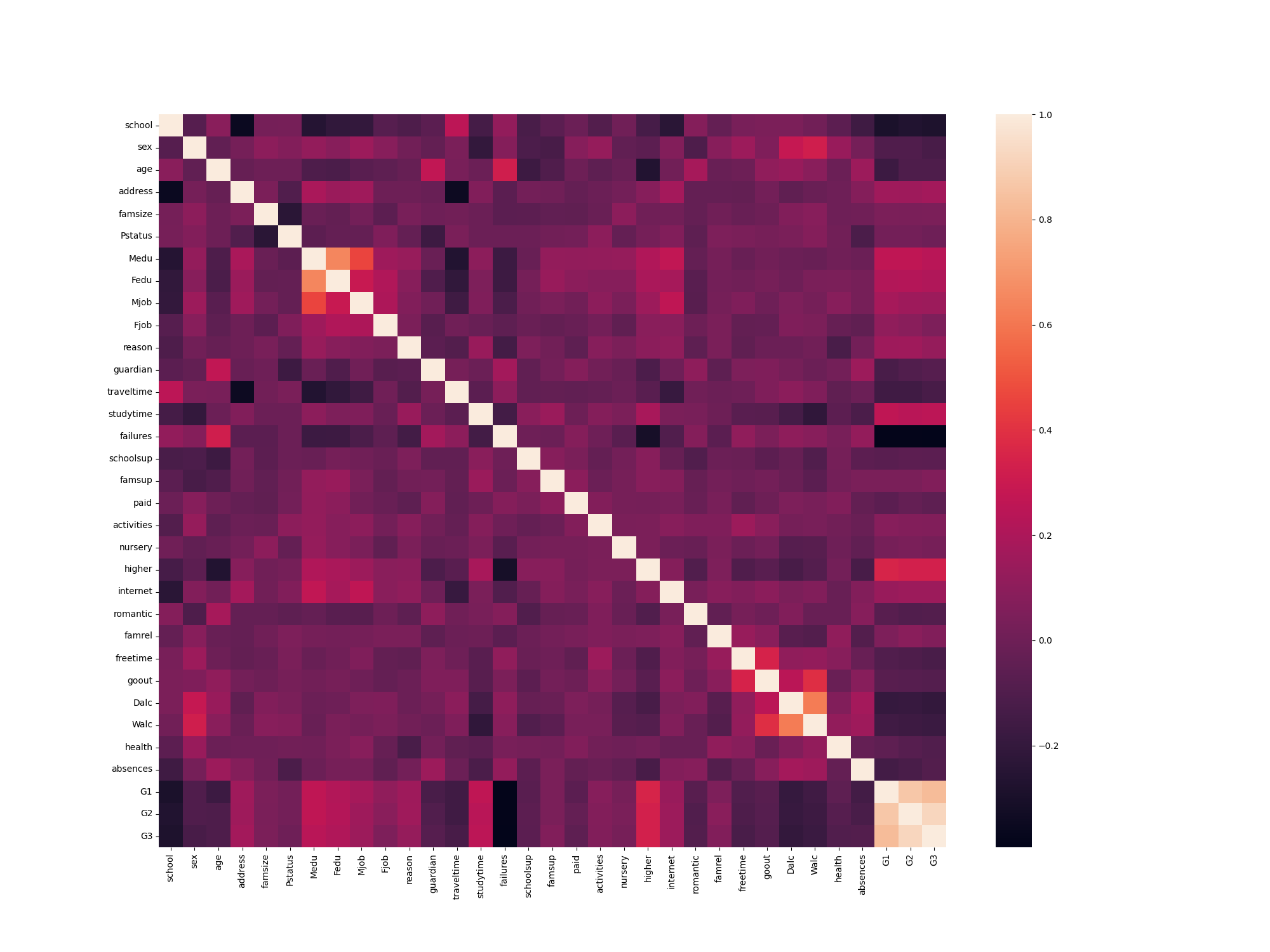
Tome um tempo para observar bem esse mapa, e entender o que ele significa e o que nos diz. Por ele, podemos observar diretamente diversas correlações, que resultam em inferências interessantes. Áreas mais claras significam maior correlação entre as variáveis.

Podemos observar que, por exemplo:

  • Existe uma correlação entre tempo livre e tempo gasto com amigos.
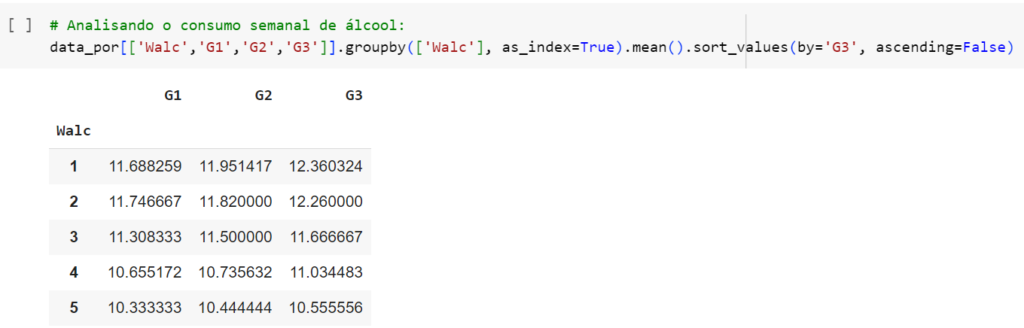
  • Existe uma correlação negativa entre consumo de álcool e tempo gasto estudando.

Use esse mapa para entender melhor os dados e fazer, você, suas próprias inferências. Mais relações podem ser inferidas a partir destes dados.

Métrica R^2 e Variáveis Dummy

Dois fatores no código à seguir devem chamar a atenção: primeiramente, o resultado R^2 Score; depois, a linha

X = pd.get_dummies(X, columns=[‘Pstatus’, ‘Fjob’], drop_first=True).

Esses itens serão explicados agora.

Métrica R^2 (lê-se R Quadrado)

Como podemos saber se nossas inferências estão corretas? Como avaliaremos se nosso modelo é preciso? Para isso, temos a métrica R^2.

De maneira simples, o chamado coeficiente de determinação, comumente representado por R², mede a proporção da variabilidade na variável dependente que é explicada pelo modelo. Ele é essencial na inferência, mas pouco útil para predições.

Ele varia de 0 a 1, onde 0 indica que o modelo não explica nenhuma variabilidade e 1 indica que o modelo explica toda a variabilidade. Obtivemos, como pode ser observado acima, uma pontuação de 0.85, que é bastante boa.

Nesse caso, um R² mais alto indica um melhor ajuste do modelo aos dados, sugerindo que uma maior porcentagem da variação na variável dependente é capturada pelas variáveis independentes incluídas no modelo.

A qualidade do R^2 está relacionada à correlação entre as variáveis. A análise de correlações pode informar a escolha de variáveis para inclusão no modelo de regressão.

O R^2 pode melhorar se incluirmos variáveis que têm uma relação substancial com a variável dependente e que não estão altamente correlacionadas entre si. Isso adiciona mais informação ao modelo, aumentando a capacidade de explicar a variabilidade na variável dependente. É interessante, para um estudo próprio do leitor, refazer o cálculo de R^2, alterando as variáveis que foram incluídas e observando a mudança no resultado final.

Variáveis Dummy

A segunda questão que chama atenção no código é a linha

X = pd.get_dummies(X, columns=[‘Pstatus’, ‘Fjob’], drop_first=True).

Essa linha é essencial para o funcionamento correto do código. Entenda: o modelo de regressão linear em scikit-learn requer que todas as variáveis de entrada sejam numéricas. Nesse caso, temos atributos ‘Pstatus’ e ‘FJob’ que são categóricos, então, precisam ser tratados.

Para lidar com variáveis categóricas, usamos técnicas como a “dummy encoding”, que nos permitem converter essas variáveis em representações numéricas.

Esse pode ser um conceito difícil de compreender bem. Em outros exemplos:

Se quiséssemos incluir a variável sexo, por exemplo, em um modelo de regressão linear, teríamos que transformar artificialmente a variável em uma variável dummy. Teríamos:

dummy_sexo = 1 em caso de sexo feminino. dummy_sexo = 0 em caso de sexo masculino.

Em um caso de variável com 3 ou mais categorias, seria necessário criar sempre n-1 dummies. Por exemplo: no caso de incluirmos a variável Estado (considerando que a base tem apenas os estados de São Paulo, Rio de Janeiro e Minas Gerais), teríamos: dummy_SP: 1 quando São Paulo e 0 nos demais dummy_RJ: 1 quando Rio de Janeiro e 0 nos demais e dummy_MG existiria quando dummy_SP e dummy_RJ são nulos.

Multicolinearidade

A multicolinearidade ocorre quando duas ou mais variáveis independentes em um modelo de regressão estão altamente correlacionadas entre si. Isso significa que uma variável pode ser linearmente prevista a partir de outras variáveis com uma alta precisão.

A multicolinearidade torna difícil para o modelo distinguir os efeitos individuais de variáveis independentes correlacionadas, e pode levar a estimativas imprecisas dos coeficientes.

Em um caso em que a multicolinearidade existe, dois principais fatores são observáveis:

  1. Pequenas mudanças nos dados podem levar a grandes variações nas estimativas dos coeficientes.

  2. Variáveis que são verdadeiramente importantes para a explicação do fenômeno podem ser erroneamente consideradas não significativas, pois a multicolinearidade torna difícil atribuir corretamente a contribuição de cada variável.

Neste exemplo, buscaremos demonstrar por meio de um mapa de calor a existência de multicolinearidade nessa base de dados.

Por meio de uma inferência básica, poderíamos deduzir “logicamente” que, alunos que tendem a se sair bem nos dois primeiros trimestres, também se sairão bem no terceiro. Provaremos isso agora:

Poderíamos assumir também, uma possível correlação entre alunos com mais tempo livre a alunos que saem mais com os amigos.

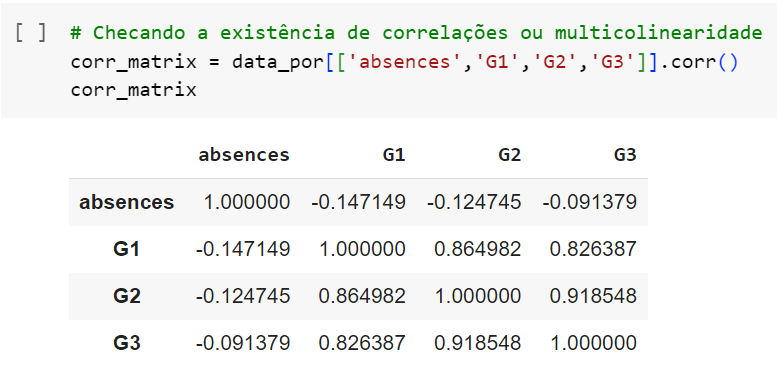
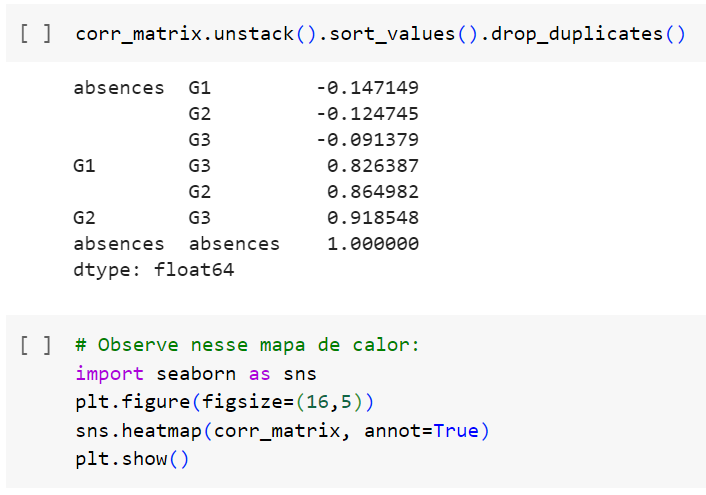
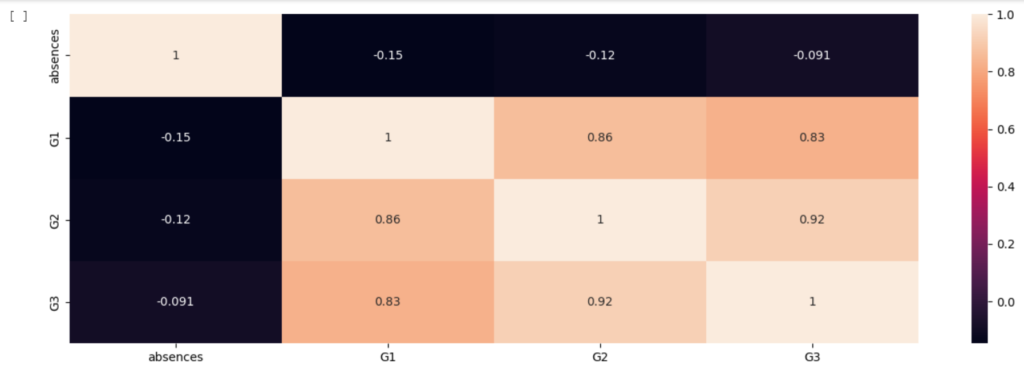
O mapa demonstra que G1 e G2 estão bastante relacionadas a G3, enquanto faltas não parecem influenciar nesses 3 atributos.

Isso não significa, necessariamente, que é impossível fazer inferências ou predições usando esses atributos. Ainda assim, eles podem causar problemas de interpretação dos coeficientes e afetar a precisão das predições.

Valor do Fator de Inflação da Variância (VIF)

Uma medida que é utilizada para avaliar empiricamente a existência de Multicolinearidade é o Valor do Fator de Inflação da Variância (VIF). É uma medida que indica o grau de multicolinearidade entre as variáveis independentes em um modelo de regressão linear.

Em termos simples, o VIF mostra quanto a variância de um coeficiente específico é aumentada devido à multicolinearidade com as outras variáveis.

Interpretamos o VIF da seguinte maneira:

Um VIF de 1 indica ausência de multicolinearidade. Geralmente, um VIF entre 1 e 5 é considerado aceitável. Um VIF acima de 5 pode indicar a presença de multicolinearidade.

Observe:

G1: O VIF de G1 é relativamente baixo, indicando que não há forte multicolinearidade entre G1 e as outras variáveis.

G2: O VIF de G2 é mais alto, indicando que há uma quantidade significativa de multicolinearidade entre G2 e as outras variáveis.

G3: G3 também tem um VIF relativamente alto, sugerindo multicolinearidade com outras variáveis.

const: A constante adicionada para calcular o VIF tem um VIF muito alto. Isso pode ser devido à multicolinearidade entre as variáveis independentes, incluindo a constante.

O que isso significa?

O VIF geralmente é comparado com um limite específico (por exemplo, 5) para avaliar a presença de multicolinearidade. Neste caso, os valores de VIF para G2 e G3 podem ser considerados relativamente altos, sugerindo multicolinearidade significativa.

Como explicamos, a multicolinearidade pode afetar a interpretação dos coeficientes de regressão, tornando-os instáveis e difíceis de interpretar.

Fim

Parabéns, voce chegou ao fim desse tutorial! Esperamos que você tenha aprendido bastante e que o conteúdo tenha sido útil em sua jornada.

Nesse estudo, utilizamos duas ferramentas muito importantes para a Estatística e Ciência de Dados no geral: O Google Colaboratory (ou Colab) e Python. Recomendamos também que o aluno pesquise e se familiarize com ferramentas como R e Matlab, para se tornar mais versado em suas habilidades.

Fontes

RYU, Thomas. Variáveis Dummy: o que é? Quando usar? E como usar?. Medium: 2019. Disponível em: https://medium.com/data-hackers/vari%C3%A1veis-dummy-o-que-%C3%A9-quando-usar-e-como-usar-78de66cfcca9#:~:text=Vari%C3%A1veis%20dummy%20s%C3%A3o%20vari%C3%A1veis%20bin%C3%A1rias%20%280%20ou%201%29,dummy_sexo%20%3D%201%20em%20caso%20de%20sexo%20feminino. Acesso em: 9 nov. 2023.

Silva, Elaine. O que é multicolinearidade?. Medium: 2023. Disponível em https://medium.com/@lainetnr/o-que-%C3%A9-multicolinearidade-e4adff76345a. Acesso em: 9 nov. 2023.

MIREIA, Irina & RUIZ, Raquel. Teste de Hipóteses: o que significa, quais são os tipos e como realizar um teste de hipóteses. Turing Talks: 2022. Disponível em https://medium.com/turing-talks/teste-de-hip%C3%B3teses-o-que-significa-quais-s%C3%A3o-os-tipos-e-como-realizar-um-teste-de-hip%C3%B3teses-1decda841bcd. Acesso em: 9 nov. 2023.

JÚNIOR, Clébio de Oliveira. Entendendo as métricas R², MAE, MAPE, MSE e RMSE. Data Hackers: Dez. 2021. Disponível em https://medium.com/data-hackers/prevendo-n%C3%BAmeros-entendendo-m%C3%A9tricas-de-regress%C3%A3o-35545e011e70#:~:text=A%20m%C3%A9trica%20R%C2%B2%2C%20tamb%C3%A9m%20conhecida%20como%20R-dois%20ou,percentuais%2C%20ou%20seja%2C%20variando%20entre%200%25%20e%20100%25. Acesso em: 9 nov. 2023.

Python Scikit-Learn. Disponível em https://scikit-learn.org/stable/. Acesso em 10 nov. 2023.

Minaei-Bidgoli B.; Kashy D.; Kortemeyer G.; and Punch W., 2003. Predicting student performance: an application of data mining methods with an educational web-based system. In Proc. of IEEE Frontiers in Education. Colorado, USA, 13–18. Acesso em 12 nov. 2023.

Hastie T.; Tibshirani R.; and Friedman J., 2001. The Elements of Statistical Learning: Data Mining, Infererence, and Prediction. Springer-Verlag, NY, USA. Acesso em 12 nov. 2023.

Cortez, Paulo. (2014). Student Performance. UCI Machine Learning Repository. https://doi.org/10.24432/C5TG7T. Acesso em 12 nov. 2023.

Student-Grades-Prediction, por Shwetago. Disponível em https://github.com/Shwetago/Student-grades-prediction/blob/master/Predicting_student_grades.ipynb. Acesso em 16 nov. 2023.

Student-Performance-Prediction, por RohithYogi. Disponível em https://github.com/RohithYogi/Student-Performance-Prediction/blob/master/README.md.Último acesso em 17 nov. 2023.

Student Performance, por Ben Gruher. Disponível em https://github.com/bengruher/Student-Performance-Prediction/blob/master/README.md. Último acesso em 17 nov. 2023.

Autores

Heitor Pavani Nolla (173233)

Nataly Stychnicki (173722)

Pedro Montagner Rezende (173779

Victor Ferreira Da Silva (177950)

Rian Júlian Braga Kökény (260664)

 

You May Also Like: