---

INTRODUÇÃO A REGRESSÃO

Em 1885, o antropólogo e estatístico Francis Galton protagonizou uma descoberta fascinante na análise estatística ao cunhar o termo “Regressão”. Essa descoberta teve suas raízes na Antropometria, o estudo meticuloso das medidas e a matemática dos corpos humanos.

REGRESSÃO LINEAR

A regressão linear, em suma, é uma técnica que busca prever o valor de dados desconhecidos usando como base valores de dados relacionados e conhecidos. 

Além disso, ao se aprofundar nessa ferramenta, saindo da teoria, é notável que ela possa ser utilizada de duas maneiras distintas: regressão linear de predição e regressão linear de classificação.

Na regressão linear de predição, o foco está em estimar ou prever valores numéricos para uma variável em específico. Em outras palavras, o interesse reside em antecipar números específicos com base em padrões identificados nos dados relacionados. Isso se revela útil em cenários como previsão de preços de ações, onde a variável em estudo é numérica e buscamos compreender as tendências futuras com base em informações históricas.

Por outro lado, na regressão linear de classificação, o propósito muda. Nesse caso, a variável é categórica, e o objetivo é classificar os dados em categorias específicas. Como, por exemplo, ao classificar o desempenho de estudantes, é possível  utilizar a regressão linear de classificação e dividir as variáveis em dois grupos distintos, aprovados ou reprovados, dessa forma,  com base nas características de estudo de cada aluno, será possível classificá-los em uma das possíveis classes.

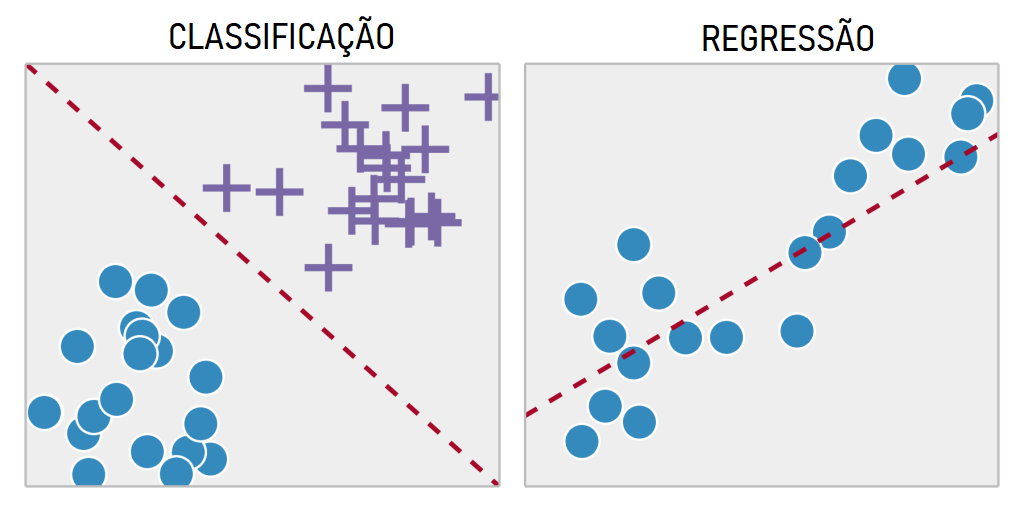
A principal diferença entre essas abordagens reside no tipo de pergunta que estamos fazendo aos dados. Quando buscamos valores numéricos, optamos pela regressão linear de predição. Se a nossa curiosidade está voltada para categorias, a regressão linear de classificação é a escolha apropriada. Em nosso caso, a técnica que estudaremos durante esse artigo será a regressão linear de predição.

Para entendermos melhor o conceito de regressão linear de predição, vamos observar a situação proposta:

“Suponha que um engenheiro industrial empregado por uma engarrafadora de bebidas analise as operações de entrega de produtos e serviços para máquinas de venda. Ele suspeita que o tempo necessário para um entregador de rota carregar e atender a uma máquina está relacionado ao número de caixas de produtos entregues. O engenheiro visita 25 pontos de venda escolhidos aleatoriamente que possuem máquinas de venda. O tempo de entrega (em minutos) e o volume de produtos entregues (em caixas) são observados para cada uma das máquinas de venda.”

Se representarmos y como o tempo de entrega e x como o volume de entrega, a equação de uma linha reta que relaciona essas duas variáveis é y = β0 + β1.x, onde β0 é a interceptação no eixo y e β1 é a inclinação da reta. Porém, os pontos de dados não se ajustam exatamente a uma linha reta, dessa forma, a equação deve ser modificada para levar isso em consideração. Esse ajuste aplicado sobre a equação trata-se da diferença entre o valores previstos pela reta e os valores observados, na qual chamamos de erro ε. É conveniente pensar em ε como um erro estatístico, ou seja, uma variável aleatória que considera a falta de ajuste exato do modelo aos dados. O erro pode ser composto pela influência de variáveis ocultas no problema, como o tempo de entrega, erros de medição e assim por diante. Portanto, um modelo mais plausível para os dados de tempo de entrega é y = β0 + β1.x + ε.  Essa é a equação da reta que define a regressão linear simples:

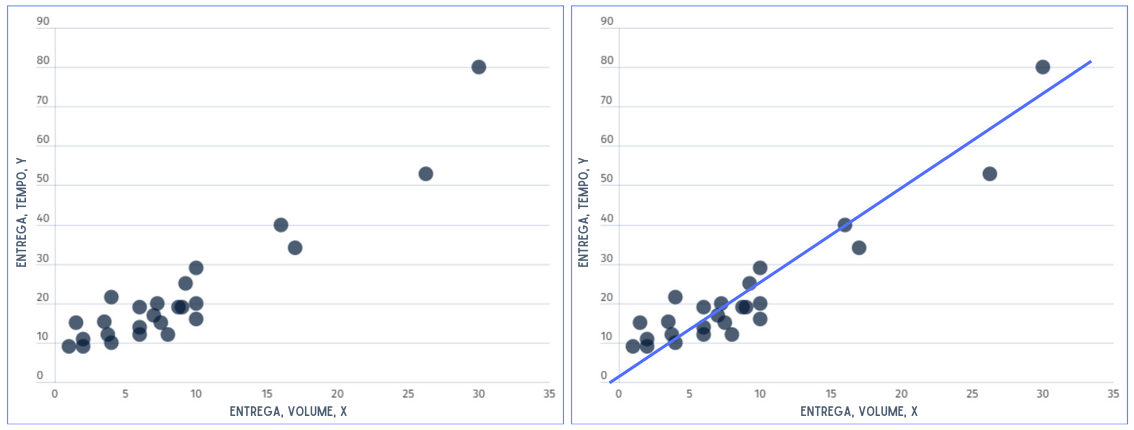
y = β0 + β1.x + ε

• y: É a variável que define a altura dos pontos previstos pela função
• β0: É a constante que determina a intersecção da reta com o eixo y, ou seja, quando x=0.
• β1: É o valor que indica a inclinação da reta, podendo ser interpretada como a mudança na média de y para uma mudança de uma unidade em x
• x: É a variável que determina a posição horizontal dos pontos previstos pela função.
• ε: É o erro estatístico, é uma variável que serve para compensar pelos possíveis erros de predição que a reta apresentará.

Esse tipo de regressão é uma linha de valores médios, isto é, representa um valor médio que esperamos para y quando x tem um valor qualquer atribuído. No modelo, x é chamado de variável independente, ou seja, é a variável manipulável que possui influência sobre a variável dependente, enquanto o  y é chamado de variável dependente, a variável que está sendo estudada ou medida, e que é influenciada por outras variáveis, as independentes. 

Dessa forma, o objetivo da Regressão Linear é encontrar os valores de β0 e β1 que minimizem a diferença entre o conjunto real de dados e o conjunto previsto pela regressão Linear. Isso pode ser obtido utilizando o método dos Mínimos Quadrados, que é uma técnica estatística usada para estimar os parâmetros de um modelo matemático, minimizando a soma dos quadrados das diferenças entre os valores observados e os valores preditos pelo modelo. Essa abordagem busca encontrar a melhor linha que se ajusta aos dados observados, minimizando a soma dos quadrados das discrepâncias verticais entre esses dados e os valores preditos pelo modelo. Essa é a equação que define as variáveis β0 e β1 com base no método dos mínimos quadrados.

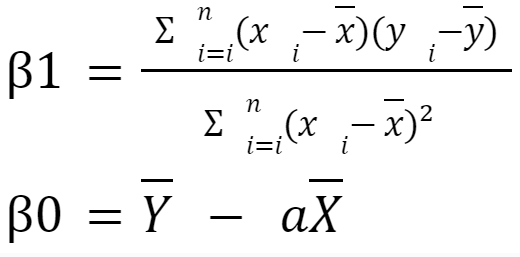
• Xi: É o valor x das variáveis independentes
• X̄: É a média aritmética das variáveis independentes
• Yi:  É o valor y das variáveis dependentes
• Ȳ: É a média aritmética das variáveis dependentes

Na equação acima, em β1, sua equação é dada como a razão entre o somatório dos produtos da diferença das observações em relação às variáveis de x, X̄ e y, Ȳ e o somatório dos quadrados da diferença de x em relação a X̄. Em suma, A razão entre a soma dos produtos da diferença entre x, X̄ e y, Ȳ e a soma dos quadrados da diferença entre x em relação a X̄ proporciona uma medida ponderada das alterações em y em resposta às mudanças em x. Isso significa que a equação reflete como as variações nas observações de x influenciam as variações correspondentes em y, estabelecendo a inclinação da linha de regressão. Quando β1 é positivo, há uma relação positiva; quando negativo, indica uma relação negativa.

Por outro lado, em β0, sua equação  é expressa como a diferença entre Ȳ  e o produto de β1 e X̄. Dessa forma a interpretação de β0 é contextual, sendo mais relevante quando x pode assumir o valor zero, que fornece uma estimativa do valor inicial esperado da variável no eixo y.

Em conjunto, essas equações possibilitam a construção de uma linha de regressão que melhor se ajusta aos dados observados, oferecendo uma representação quantitativa da relação linear entre as variáveis. A interpretação desses coeficientes é essencial para compreender como as mudanças em uma variável estão associadas às mudanças na outra, fornecendo uma base sólida para análises preditivas e inferências estatísticas

PRESSUPOSIÇÕES DA REGRESSÃO

Apesar de sua aparente simplicidade, a regressão linear se baseia em pressuposições, isto é, em cinco fatores fundamentais que devem ser satisfeitos para que os resultados sejam válidos.

A primeira e fundamental premissa é a linearidade, que postula que a relação entre a variável dependente e as variáveis independentes é verdadeiramente linear, ou seja, as mudanças nas variáveis independentes provocam variações proporcionais na variável dependente, esboçando uma trajetória linear. Esta linearidade não apenas guia o modelo, mas também assegura a interpretação adequada dos resultados.

Seguindo adiante, a independência dos erros surge como uma premissa vital. Ela estabelece que deve haver pouca ou nenhuma autocorrelação nos dados. A autocorrelação é um fenômeno que ocorre quando os erros, a discrepância entre os dados previstos e os reais não são independentes entre si. Por exemplo, isso é comum em preços de ações, onde o preço atual não é independente do preço anterior. Dessa forma, essa assunção garante uma acurácia maior para o algoritmo.

A homocedasticidade é uma condição frequentemente negligenciada, mas essencial. Ela garante que a dispersão dos erros seja uniforme em todas as partes do conjunto de dados, evitando oscilações desiguais nas previsões que comprometeriam a confiabilidade das estimativas, dessa maneira, assegurando a previsibilidade dos erros no conjunto inteiro, e consequentemente assegurando a previsibilidade da regressão linear.

No jogo de variáveis independentes, a multicolinearidade é uma consideração crítica. Ela exige que cada variável independente contribua de maneira única para as previsões, sem interferir em relação às outras, do contrário,seria desafiador, beirando a impossibilidade, discernir o impacto individual de cada variável independente sobre a variável dependente.

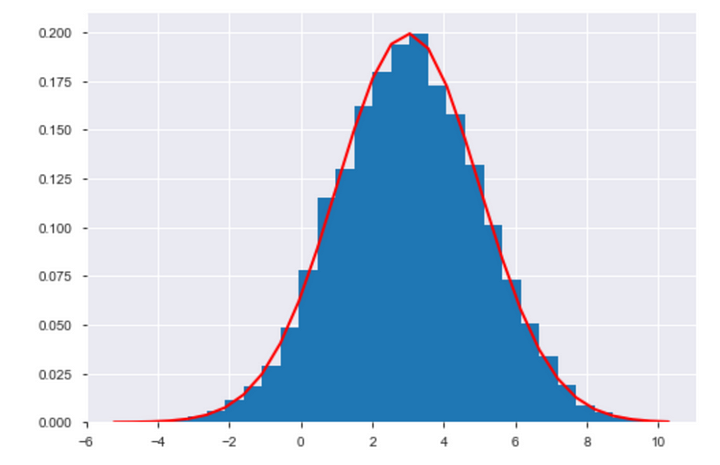
Por fim, a normalidade dos erros é vital para as inferências estatísticas. Ela supõe que a diferença entre os valores observados e os valores previstos seguem uma distribuição normal, ou seja, significa que os erros cometidos pelo modelo devem se aproximar de uma distribuição de sino, também conhecida como distribuição normal ou gaussiana. Essa suposição é crucial pois quando os erros têm uma distribuição normal, é possível aplicar métodos estatísticos mais confiáveis para avaliar a precisão do modelo e realizar inferências sobre os parâmetros da regressão.

MÉTODO DOS MÍNIMOS QUADRADOS

A determinação dos parâmetros é essencial, uma vez que esses valores estabelecem tanto a inclinação quanto a interceptação da linha de regressão, permitindo com que a aplicação do modelo para efetuar previsões e inferências acerca da relação entre as variáveis.

Dentre os métodos empregados para validação, destaca-se o Método dos Mínimos Quadrados. Nota-se que os parâmetros β0 e β1 são desconhecidos e precisam ser estimados. O método dos mínimos quadrados é utilizado justamente para estimar β0 e β1.

Para estimar esses valores, partimos do pressuposto de que temos n pares de dados (y₁, x₁), (y₂, x₂), …, (yₙ, xₙ). O método é então utilizado para ajustar uma linha aos dados de maneira a minimizar a soma dos quadrados das diferenças entre as observações yᵢ e a reta y = β0 + β1.x + ε, alcançando assim o melhor ajuste possível aos dados.

Portanto, o método visa minimizar a expressão:

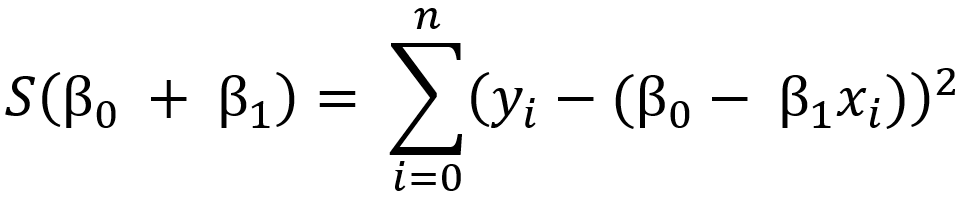
O objetivo do método é encontrar os parâmetros β₀ e β₁ que minimizam essa soma. Quando esses valores são encontrados, a linha de regressão resultante tenta ser a que melhor se ajusta aos dados, diminuindo a discrepância entre os valores observados e os valores previstos pela linha.

UM POUCO SOBRE CORRELAÇÃO DOS DADOS

Outro conceito importante é o quão boa a correlação linear entre dados pode se apresentar, ou seja, quando o relacionamento entre os dados (positivo ou negativo) pode ser definido com uma reta. A análise de correlação mede a “intensidade” de relacionamento linear entre as variáveis X e Y. Para quantificar a relação entre essas duas variáveis quantitativas utiliza-se o coeficiente de correlação linear de Pearson.
Este que por sua vez é representado pela seguinte equação:

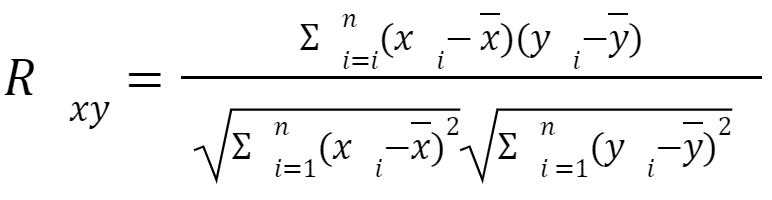
Em que:

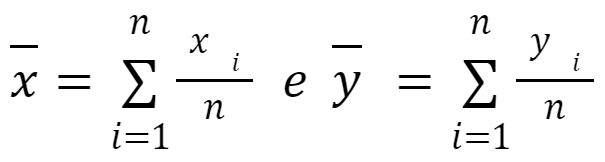
Pode-se inferir, com base em R_xy, sobre a direção e intensidade da relação entre X e Y. Por não haver uma classificação unânime da correlação. Foi optado por seguir a fórmula apresentada por Santos (2007), conforme indicado na Tabela.

Para entender a relação entre duas variáveis, X e Y, é possível representar os valores delas num gráfico de dispersão. Pode-se confirmar que existe uma relação linear entre essas variáveis se os dados mostrarem proximidade com uma linha reta. Como mostrado nos gráficos abaixo.

---

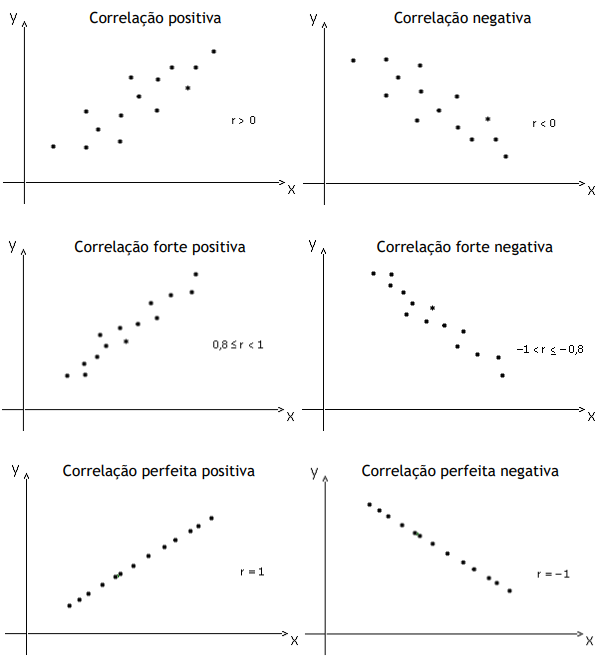
APLICAÇÃO COM PYTHON

Agora que entendemos como funciona a regressão linear, vamos realizar um exemplo de problema de predição em Python! O exemplo que iremos usar será o mesmo apresentado no começo deste artigo sobre o engenheiro industrial, então vamos começar do início:

1) CONHECENDO O COLAB

O primeiro passo é escolher o ambiente onde iremos escrever nosso código. No exemplo, iremos usar o Google Colaboratory, conhecido pela comunidade como Colab. Ele é uma ferramenta que permite trabalhar com códigos que envolvam análise de dados, machine learning, e outras tarefas relacionadas à ciência de dados. O Colab é projetado para trabalhar principalmente com Python.

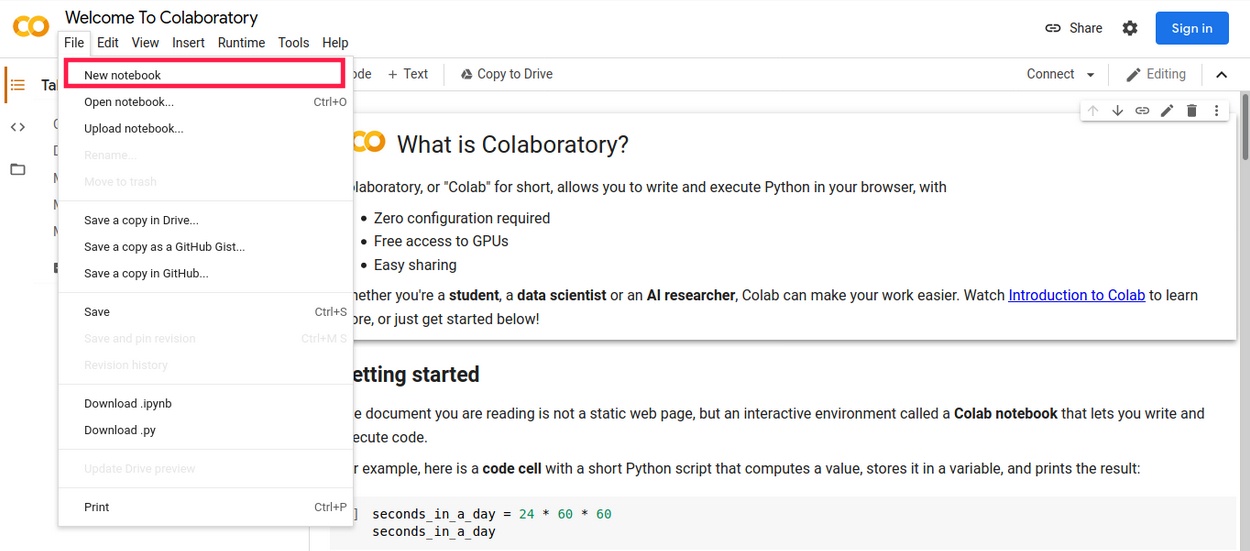
2) COMO CRIAR UM NOTEBOOK

O “notebook” no contexto do Google Colab refere-se a um documento interativo na qual iremos escrever nossos códigos.

É necessário estar logado em uma conta google para criar um notebook, pois ele ficará atrelado a seu perfil, permitindo que possa revisitar o notebook a qualquer momento.

3) PRIMEIRAS LINHAS DE CÓDIGO: BUSCANDO BIBLIOTECAS

Nossas primeiras linhas de código referem-se a chamadas das bibliotecas que iremos usar no código. As bibliotecas do Python são conjuntos de código predefinido que fornecem funcionalidades específicas, permitindo que você use-os sem ter que escrevê-los do zero. 

Algumas das bibliotecas usadas são:

• pandas (pd): permite a manipulação e análise eficiente de dados
• numpy (np): suporte para arrays multidimensionais e funções matemáticas eficientes
• seaborn (sns) e matplotlib.pyplot (plt): bibliotecas de visualização que facilitam a criação de gráficos e visualizações
• sklearn: oferece uma variedade de ferramentas para tarefas relacionadas à mineração de dados e aprendizado de máquina

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
from matplotlib import pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression

4) CRIANDO UM DATAFRAME COM OS PONTOS DO PROBLEMA

Vamos agora criar o DataFrame com os pontos do problema do engenheiro. Fazendo uma aproximação por observação do gráfico, chegamos nos 25 pontos de venda descritos.

column_titles = ['x','y']
coordenadas_bolinhas = np.array([[1,9],
[2,9],
[4,10],
[2,11],
[1.5,15],
[3.75,12],
[3.5,15.25],
[6,12],
[6,14],
[4,21.5],
[6,19],
[8,12],
[7.5,15],
[7,17],
[7.25,20],
[8.75,19],
[9,19],
[10,16],
[10,20],
[9.25,25],
[10,29],
[16,40],
[17,34],
[26.25,53],
[30,80]])
df = pd.DataFrame(data=coordenadas_bolinhas, columns=column_titles)
df

A saída de df deve ser:

	x		y       
0	1.00	9.00
1	2.00	9.00
2	4.00	10.00
3	2.00	11.00
4	1.50	15.00
5	3.75	12.00
6	3.50	15.25
7	6.00	12.00
8	6.00	14.00
9	4.00	21.50
10	6.00	19.00
11	8.00	12.00
12	7.50	15.00
13	7.00	17.00
14	7.25	20.00
15	8.75	19.00
16	9.00	19.00
17	10.00	16.00
18	10.00	20.00
19	9.25	25.00
20	10.00	29.00
21	16.00	40.00
22	17.00	34.00
23	26.25	53.00
24	30.00	80.00

5) SEPARANDO OS DADOS EM TREINO E TESTE E PLOTANDO O GRÁFICO DE DISPERSÃO

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(df[['x']], df['y'], test_size=0.2, random_state=0)

# Create and fit the linear regression model
model = LinearRegression()
model.fit(X_train, y_train)

# Make predictions on the test set
y_pred = model.predict(X_test)

# Plot the training points
plt.scatter(X_train, y_train, color='g', label='Training Data')

# Plot the linear regression line for the test set
plt.plot(X_test, y_pred, color='k', label='Linear Regression Line')

# Create a legend for the graphic
plt.legend()
plt.show()

Uma das etapas da mineração de dados envolve a separação de nossa base de dados em dois conjuntos, o grupo de treino e o grupo de teste. O conjunto de dados separados para treino são os dados que serão usados para treinar o algoritmo que de regressão linear que iremos usar. Já o conjunto de testes, será usado posteriormente para avaliar o desempenho do modelo em dados não vistos.A função usada para fazer essa separação é do sklearn e se chama “train_test_split”.

Logo em seguida, criamos  uma instância do modelo de regressão linear com “LinearRegression()“, passando os dados do conjunto de treinamento com o método “.fit” ao modelo. É interessante saber que o Método dos Mínimos Quadrados é automaticamente utilizado quando você ajusta um modelo usamos o método “fit”, ajustando assim o modelo aos dados de treinamento.

Com o modelo treinado, podemos ver os dados que vão ser preditos pelo algoritmo com o método “.predict“. Armazenamos esses valores preditos na variável “y_pred“.

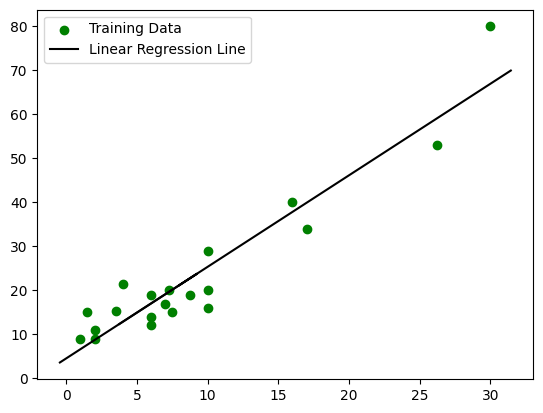
Usamos então o matplotlib para criar um gráfico de dispersão dos pontos de treino (verde) e plotar a linha de regressão linear prevista nos dados de teste (preto). Também incluímos uma legenda ao gráfico para indicar os dados de treinamento e a linha de regressão linear.

O resultado de saída é o gráfico plotado, porém pode existir uma problema com a extensão da linha de regressão, que pode acabar não indo até o final do gráfico. Isso deve ocorrer devido a quantidade limitada de dados na extremidade do eixo x, que faz o modelo ter dificuldade em estender a linha de maneira significativa.

Para corrigir a extensão da linha e gerar uma melhor visualização, podemos ajustá-la para cobrir toda a largura do gráfico. Usamos o método “plt.xlim()” para fazer essa configuração.

# [...]

# Plot the linear regression line for the test set
plt.plot(X_test, y_pred, color='k', label='Linear Regression Line')

# Extend the line to cover the entire width of the graph
x_min, x_max = plt.xlim()
x_extend = np.linspace(x_min, x_max, 100)
y_extend = model.coef_[0] * x_extend + model.intercept_
plt.plot(x_extend, y_extend, color='k')

# [...]

A saída do gráfico fica:

6) VERIFICANDO PODER DE PREVISÃO DO MODELO

Vamos agora utilizar uma métrica para sabermos qual o poder de previsão do nosso modelo. Para tal tarefa, vamos usar uma função bastante popular que é o cálculo do R² usando a função ” r2_score“. Essa métrica fornece uma medida que varia de 0 a 1 (na qual 1 indica o ajuste perfeito). Essa medida diz o quão bem as previsões do modelo se ajustam aos dados reais.

Comparamos os valores reais (y_test) com as previsões do modelo (y_pred) e atribuímos essa comparação à variável “r_squared”.

r_squared = r2_score(y_test, y_pred)
print(f"R-squared (R^2) Score: {r_squared}")

R-squared (R^2) Score: 0.2875287223839458

O resultado obtivo mostra que modelo explica aproximadamente 28,75% da variabilidade nos dados de teste, o que não é um valor considerado satisfatório para a métrica.

7) PREVENDO UM VALOR

Para fecharmos o exemplo proposto, vamos fazer uma previsão usando o modelo de regressão linear treinado. Usamos o método “model.predict“, passamos um valor x para qual será correspondido com um valor previsto y.

new_x_value = 5.0  # Replace with the desired 'x' value
new_x_value = [[new_x_value]]
predicted_y = model.predict(new_x_value)
print(predicted_y)

[14.93059242]

EXEMPLO COM MELHOR PREVISÃO DO MODELO

O problema mostrado acima traz um impecilho, seu poder de previsão para se ajustarem aos dados reais é muito fraco. Isso aconteceu porque a quantidade de dados passado para treinar o modelo era muito pequeno. Por isso, vamos agora usar outra base de dados que contenha uma quantidade considerada de dados para o treino.

A base de dados usado se trata de uma disponibilizada pelo kaggle, que é plataforma focada para conteúdos de aprendizado de máquina. Chamada de “Experience Salary Dataset” se trata sobre a relação entre a experiência profissional (em meses) e os salários mensais correspondentes (em milhares de dólares) de funcionários em vários setores.

A base de dados possui 1000 instâncias, o que ainda pode ser considerado poucos dados para treinar um modelo, mas para o exemplo podemos ver o salto significativo do cálculo da precisão.

df = pd.read_csv('Experience-Salary.csv')

quantidade_instancias = df.shape[0]
print("Número de instâncias na tabela:", quantidade_instancias)

Número de instâncias na tabela: 1000

Agora fazemos os mesmos passos do exemplo anterior, na qual treinamos o modelo e plotamos o gráfico.

X = df[['exp(in months)']]
y = df['salary(in thousands)']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

model = LinearRegression()


model.fit(X_train, y_train)
y_pred = model.predict(X_test)
plt.scatter(X_train, y_train,color='g')
plt.plot(X_test, y_pred,color='k')

plt.show()

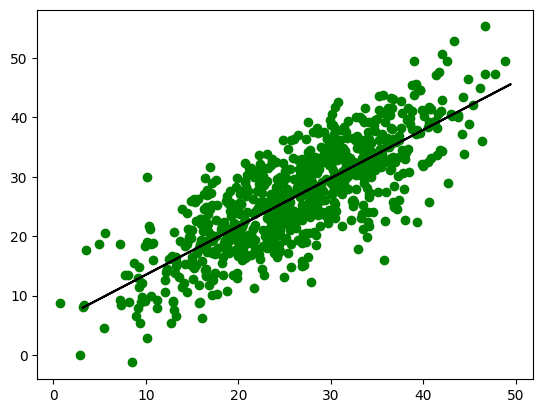
Comparando os valores reais (y_test) com as previsões do modelo (y_pred), o r_squared nos mostra uma acurácia de aproximadamente 74%, uma porcentagem considerada positiva para o modelo.

 from sklearn.metrics import  r2_score
r_squared = r2_score(y_test, y_pred)
print(f"R-squared (R^2) Score: {r_squared}")

R-squared (R^2) Score: 0.746188470890027

---

REFERÊNCIAS

[1] MONTGOMERY, Douglas C.; PECK, Elizabeth A.; VINING, G. Geffrey. Introduction to Linear Regression Analysis. 5. ed. Wiley Series in Probability and Statistics. Wiley.

Autores

Henrique Yugo Saito (172299)

Marx Maciel Xavier (184878 )

Isabella Carolina Silva De Araújo (254264)

Jorge Yudi Saito Maruyama (254274)